普段、私たちが見ているこの世界。
ほんの少しだけ「数学」を知ってみると、意外な奥行きが見えてくるかもしれません。
今回は「17世紀の学術サークル」のお話から、数学の歴史を覗いていきます。
仲間が集まり、議論し、互いに刺激を受けて高め合う……そんな場が大切なのは今も昔も変わりません。特に、最近では「コミュニティ」という言葉が一般的になり、仕事やプライベートで「コミュニティづくり」や「コミュニティ運営」に関わっている人が増えてきていますよね。
数百年も前の事例ですが、「17世紀の学術サークル」もコミュニティの一つ。そこには、現代の私たちが学べることがあるかもしれません!
侮れない!サークル活動
あなたはサークル活動をした経験はありますか?

「学生時代に軽音サークルに所属していました」「社会人になってから、フットサルサークルに入りました」など、何かしらのサークル活動経験がある方は多いのではないでしょうか。
サークル活動の目的は、趣味の追及・息抜き・友だちづくりなど、人によって様々ですよね。
中には「サークルのおかげで、精神的に救われました」「サークルで知り合った人と結婚しました」など、サークル活動がきっかけで、人生が変わった人もいると思います。
さらには、サークル活動が、自分の人生だけでなく、社会や歴史に大きな影響を与えることもあります。
例えば、大学のサークルで社会問題に関する勉強会をしてSNSで発信していたら、大きなムーブメントになり行政が動き始めた……なんてことも、このご時世、十分起こり得ます。
そう考えると、サークル活動は侮れない存在ですよね。
今回紹介する「17世紀の学術サークル活動」も、その影響力は絶大。数学史を語る上で、なくてはならない存在となったのです。
偉大な数学者たちが関わっていた!17世紀の学術サークル
舞台は17世紀のヨーロッパ。

現代のようにインターネットなどの通信手段や、飛行機などの便利な交通手段のなかった時代です。さらに、17世紀初頭は、数学の論文を発表する雑誌なども存在していませんでした。
そのため、「数学の成果を発表すること」や「数学の成果を知ること」は簡単なことでありません。例えば、「素晴らしい公式を発見したぞ!」という人がいても、その人がその公式を広く知らせることが非常に難しいのです。それでは、数学の発展が妨げられてしまいますよね。
しかし、フランスの神学者メルセンヌを中心とした学術サークルでは、ヨーロッパの数学者たちが国を越えて交流し、成果を知らせ合っていたのです。このことは、数学の歴史上、非常に重要な意味を持つことになりました。
しかも、メルセンヌのサークルには、歴史に名を残す偉大な数学者たちが関わっていたのです!
例えば、「数論の父」と呼ばれるフェルマーもその一人。
フェルマーは、20世紀末まで未解決問題だった「フェルマーの最終定理」で知られる大数学者です。1636年頃からメルセンヌのサークルと関わるようになり、以後、彼はヨーロッパ中に知れ渡っていくこととなりました。
その他にも、「我思う、ゆえに我あり」で有名なデカルトも、メルセンヌのサークルに関わっていた一人です。
デカルトは哲学者として有名ですが、数学者としても素晴らしい業績を残しています。
このフェルマーとデカルトは、メルセンヌのサークルを通じて、論戦になったことがあります。あまり穏やかな話ではありませんが、一流の数学者たちが議論できる機会があったのも、サークルの存在があってこそのことなのかもしれませんね。
このメルセンヌのサークルは、後のルイ14世の時代になると、フランス科学学士院へと発展していきました。
現代でも研究され続けている「メルセンヌ数」
17世紀に研究者たちの架け橋となったメルセンヌ。彼の名前は「メルセンヌ数」という数学用語で、現在でもよく知られています。
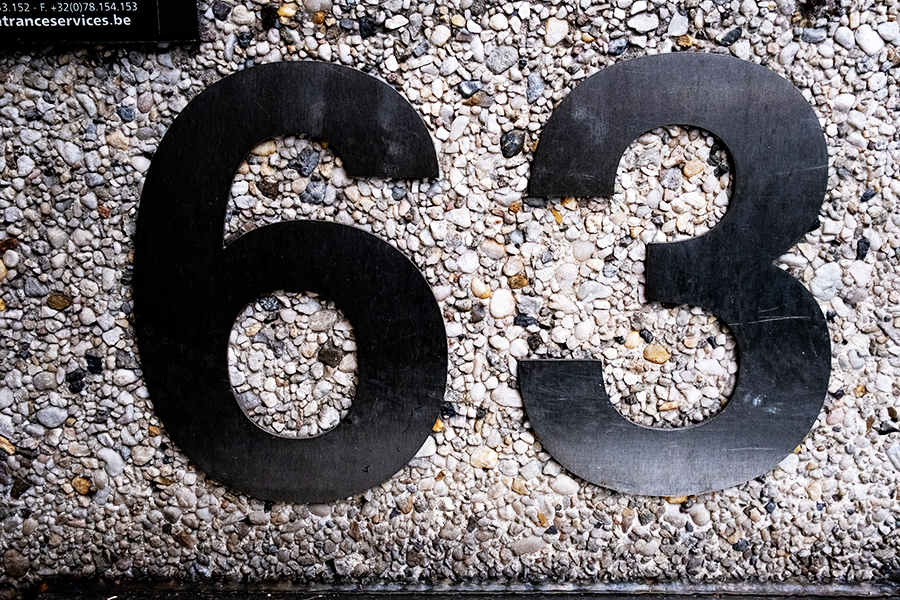
メルセンヌ数は
\[
2^n-1 \quad (n=1,2,3,4,5,\cdots)
\]
で表される数のことです。
具体的に書くと
\(1\)(\(n=1\)のとき、\(2^1-1=1\))
\(3\)(\(n=2\)のとき、\(2^2-1=3\))
\(7\)(\(n=3\)のとき、\(2^3-1=7\))
\(15\)(\(n=4\)のとき、\(2^4-1=15\))
\(31\)(\(n=5\)のとき、\(2^5-1=31\))
\(63\)(\(n=6\)のとき、\(2^6-1=63\))
\(127\)(\(n=7\)のとき、\(2^7-1=127\))
といった数のことです。
特に、メルセンヌ数の中で素数であるものを「メルセンヌ素数」と言います。
※素数とは、1より大きい整数で、1と自分自身以外に約数を持たないもののことです。
先ほど挙げた中では、3, 7, 31, 127がメルセンヌ素数です。
実は、この「メルセンヌ素数」については未だ解明されていないことがあり、現在も様々な研究が行われています。
例えば、「メルセンヌ素数は無限に存在するか?」という問題は、有名な未解決問題です。また「コンピュータで大きなメルセンヌ素数を探す」という研究も行われており、2018年には新たな最大のメルセンヌ素数が発見され、話題となりました。その桁は2486万2048桁!ここにはとても書ききれない大きな数です。
21世紀の現在も研究され続けているメルセンヌ数、十分にすごい存在ですよね。
しかし、数学の本を見てみると、以下のような記述がありました。
ミニム派修道士メルセンヌは『メルセンヌ数』という名前で現在でも知られているが、この人の果たした数学研究者間の取持ちという役割は、歴史的にはメルセンヌ数よりはるかに大きな意義を持っている(後略)
引用元 足立恒雄「フェルマーの大定理 整数論の源流[第2版]」p.39
この記述から、メルセンヌのサークルがいかに重要であったかがわかりますね!
便利な通信手段や交通手段のない時代に、数学者たちを繋げた裏側には、きっと計り知れない努力があったことでしょう。
2021年の現在は、インターネットを通じて世界中の人と知り合うことができる時代。さらに最近ではコロナ禍の影響で、便利なオンラインツールがより一層広まりました。そう思うと、サークル活動やコミュニティづくりにおいて、様々な工夫ができそうです。
メルセンヌへ敬意を表しつつ、21世紀の私たちにできることを考えていきたいですね!
※参考文献
●足立恒雄「フェルマーの大定理 整数論の源流[第2版]」(日本評論社)
●彌永昌吉「ガロアの時代 ガロアの数学 第一部 時代篇」(丸善出版)
●GIMPS「List of Known Mersenne Prime Numbers」(2021/6/10参照)
https://www.mersenne.org/primes/