普段、私たちが見ているこの世界。
ほんの少しだけ「数学」を知ってみると、意外な奥行きが見えてくるかもしれません。
鬼滅の刃 禰豆子の着物の柄「麻の葉模様」

鬼滅の刃 禰豆子の着物の柄で注目されている「麻の葉模様」。日本の伝統的な和柄です。
直線が織りなす形状が、葉っぱや葉脈のように見えます。規則的かつ幾何学的な中に、有機的な植物を思わせる美しい模様です。
今回は、この美しい模様を「数学」の視点から探ってみることにします。
同じ図形が隙間なく敷きつめられている
「麻の葉模様」では、全く同じ図形が、タイルのように隙間なく敷きつめられています。その図形は「内角が30°・30°・120°の二等辺三角形」です。
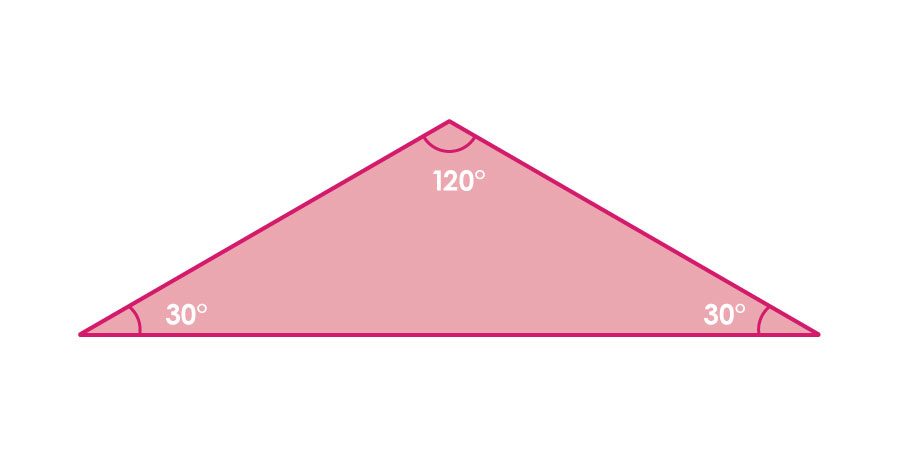
この二等辺三角形を三つ組み合わせることにより、「正三角形」ができます。
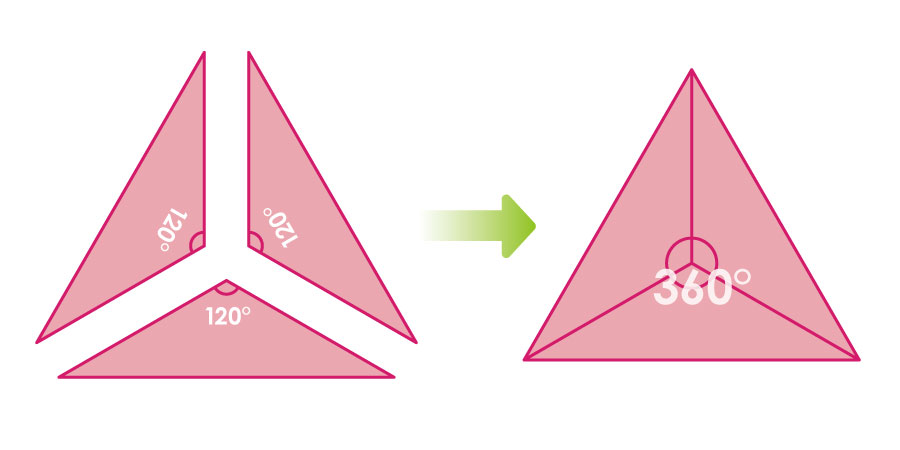
注目してほしいのは、真ん中の角度です。120°を三つ組み合わせることで、ピタリと360°になっています。
この正三角形を六つ組み合わせることによって、「正六角形」ができます。
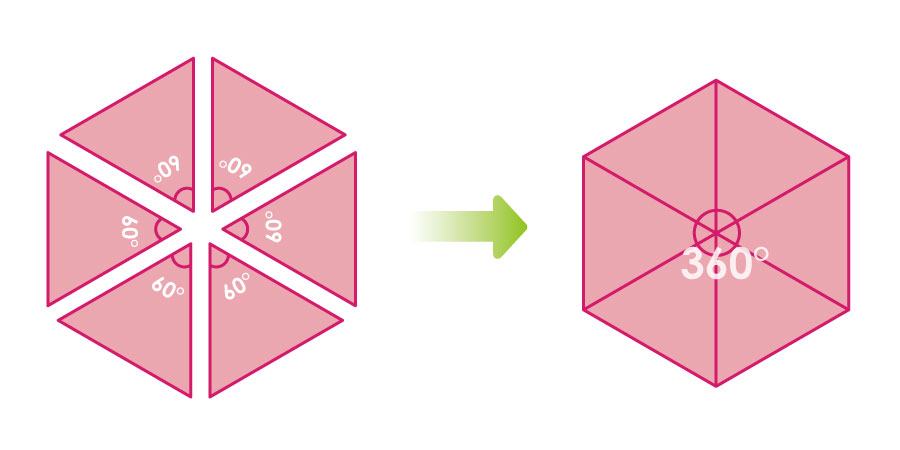
ここでも注目してほしいのは、真ん中の角度です。正三角形の内角である60°を六つ組み合わせることで、ピタリと360°になっています。
今度は、この正六角形を三つ組み合わせてみます。
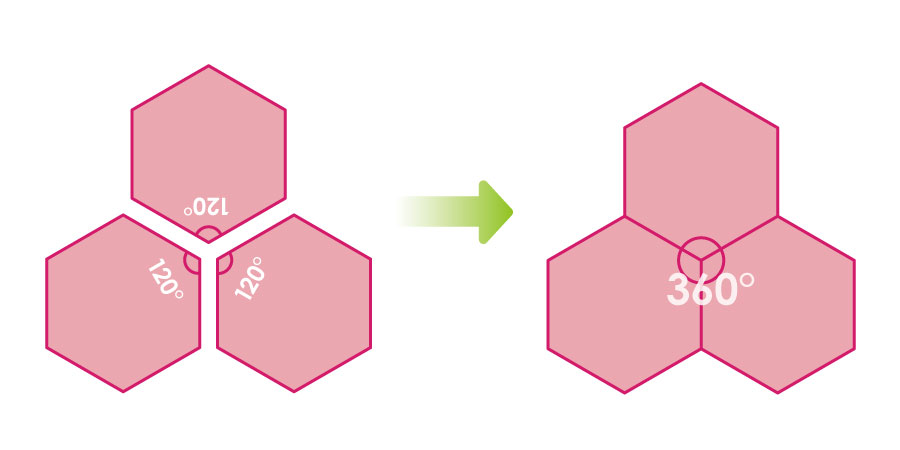
正六角形の内角は120°なので、三つ組み合わせることで、ピタリと360°になります。
これを繰り返して、たくさんの正六角形を組み合わせていくと、蜂の巣のような構造が見えてきます。タイルのように、正六角形が平面を隙間なく覆いつくすのです。

このような「平面内を同じ図形で隙間なく敷きつめること」はいつでもできることではありません。例えば、正五角形で試してみると・・・
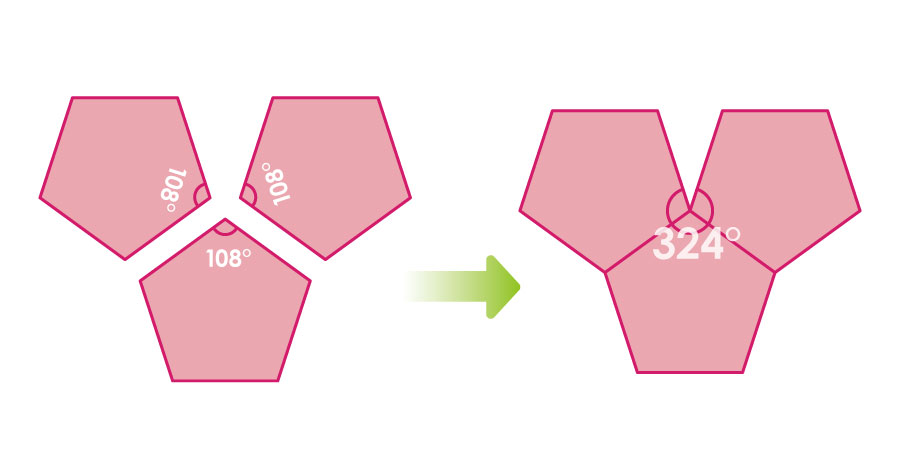
正五角形の内角は108°なので、正五角形を三つ組み合わせてみると、324°となります。そのため、先ほどのようにピタリと360°とはならず、うまくいきません。
平面充填
「平面内を有限種類の図形で隙間なく敷きつめること」を、数学では「平面充填」といいます。「麻の葉模様」は1種類の図形(内角が30°・30°・120°の二等辺三角形)による平面充填の例になっています。
鬼滅の刃 炭治郎の羽織の模様である市松模様も、正方形が隙間なく敷きつめられているため、1種類の図形による平面充填の例です。

鬼滅の刃 善逸の羽織を思わせる鱗柄も、正三角形が隙間なく敷きつめられているため、1種類の図形による平面充填の例です。

実は、1種類の正多角形による平面充填は「正三角形・正方形・正六角形」の三つ以外ではできないことが証明されています。
もちろん、今回取りあげたもの以外にも、多種多様な「平面充填」が存在しています。

例えば、オランダの画家エッシャーはペリカンやペガサスをモチーフとした見事な平面充填を描いています。他にも、2020年にノーベル物理学賞を受賞したロジャー・ペンローズが考案した「ペンローズ・タイル」も有名です。周期的なパターンがない平面充填で、エキゾチックで面白味のある模様が織りなされます。
石畳や布巾の刺繍など、きっとあなたの周りにも「平面充填」は存在しているはず。ぜひ、探してみて下さいね。