普段、私たちが見ているこの世界。
ほんの少しだけ「数学」を知ってみると、意外な奥行きが見えてくるかもしれません。

今回、紹介するのは「足し算」です。

「え？足し算？小学校で習うし、簡単だよね？」と思った方もいるかもしれません。
いえいえ！実は、足し算って、かなり奥深いんです。

今回は、なんと「無限に」足し算をしてみます！果たして、何が起こるのでしょうか？

塵も積もれば山となる！500円貯金

500円貯金をしたことがありますか？
貯金箱さえあれば手軽に始められ、「1日500円」と少額な貯金ですが、続けて行くと、かなり大きな金額になります。

1ヶ月（30日）続ければ、1万5000円。1年（365日）続ければ、18万2500円。5年半ほど続ければ、なんと100万円に到達します！

まさに「塵も積もれば山となる」ですね。「500+500+500+500+…」という足し算をし続けて行けば、どんどん数が増えていきます。

もしも、いくらでも長く生きられれば、500円貯金で1000万円、さらには1億円にだって到達することも可能ですよね！

こんな風に500円貯金の例を見てみると、「正の数を無限に足し続けたら、どんどん果てしなく数は大きくなる」と、思えます。

「そんなこと、当たり前じゃない？」という気もしますが……果たして、本当にそうなのでしょうか？

1+1/2+1/4+1/8+1/16+1/32+⋯は何になる！？

こんな足し算を考えてみましょう。

\[
1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}+\cdots
\]

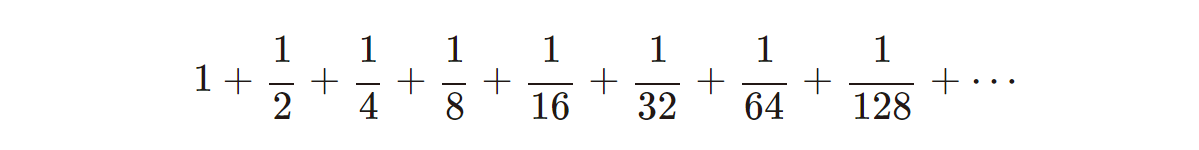
という無限に続く足し算です。

足していく数の分母が、「\(1,2,4,8,16,32,64,128,\cdots\)」と2倍されていっています。分母が大きくなっていき、足していく数は、徐々に小さくなっていきますよね。

実際に、足し算を続けて行ったら、どのような数になるか計算してみましょう。すると……

\begin{align*}
1+\frac{1}{2}&=1.5\\
1+\frac{1}{2}+\frac{1}{4}&=1.75\\
1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}&=1.875\\
1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}&=1.9375\\
1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}&=1.96875\\
1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}&=1.984375\\
1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}&=1.9921875\\
\end{align*}

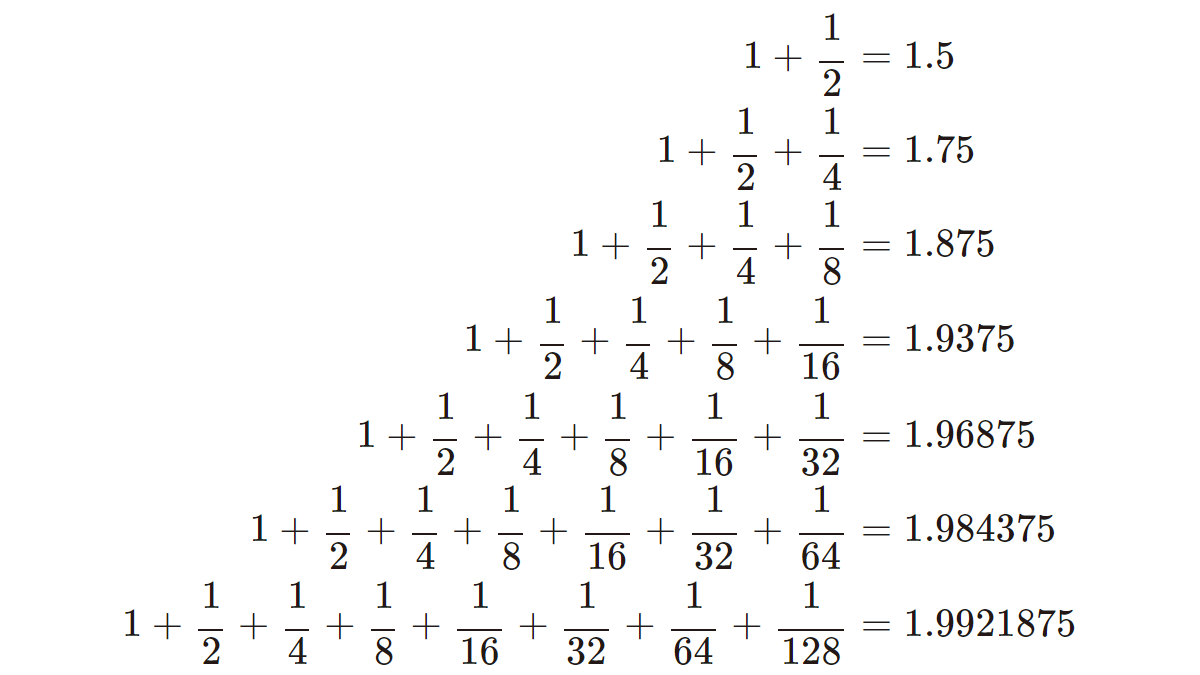
増加の具合は徐々に小さくなっていきますが、足し算を続けて行くので、じわりじわりと数は増え続けていきますね。このまま続けて行くと、どんどん果てしなく大きな数になっていくように思えます。

しかし、実際は……

\[
1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}+\cdots=2
\]

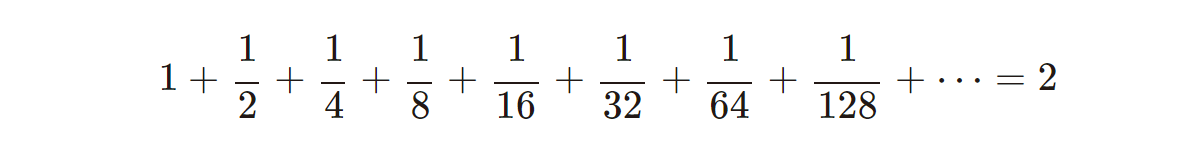
となるのです！

無限に足し続けていくのに、「\(2\)」にしかなれないなんて！なんだか不思議ですね。

このことを確認するために、図形を用いて考えてみましょう。

まず、面積「\(1\)」の正方形を二つ準備します。

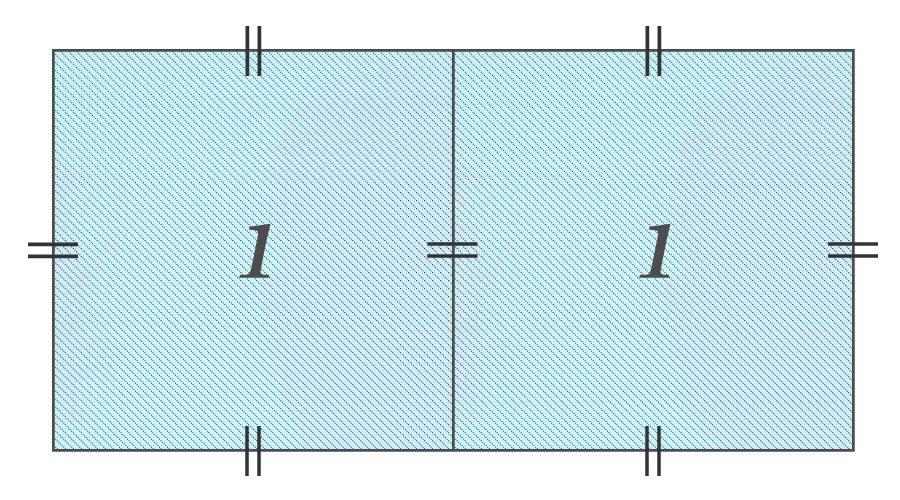
次に、右側の面積「\(1\)」の正方形を半分にして、面積「\(\frac{1}{2}\)」の長方形をつくります。

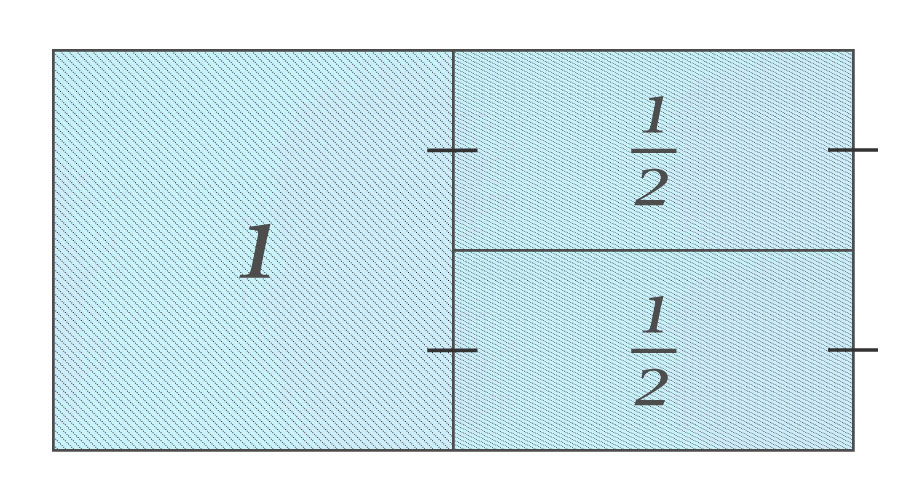
さらに、この面積「\(\frac{1}{2}\)」の長方形を半分にして、面積「\(\frac{1}{4}\)」の正方形をつくります。

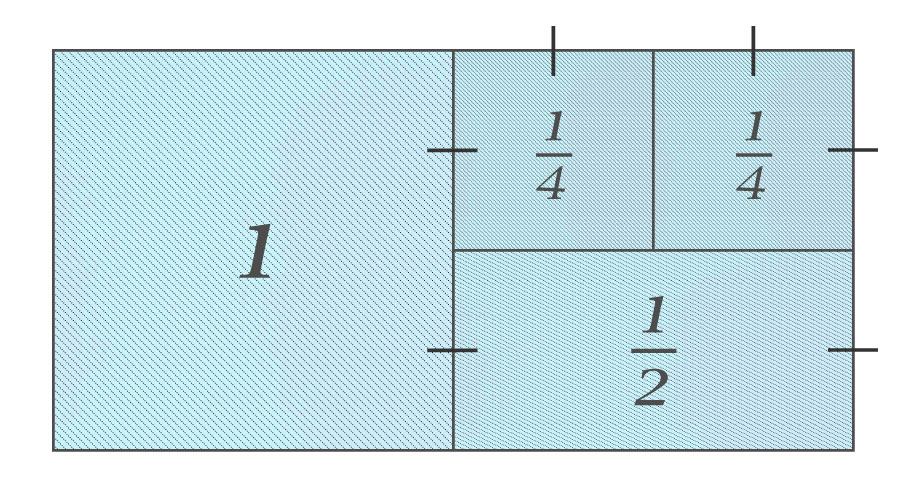
同様にして、面積「\(\frac{1}{4}\)」の正方形を半分にして、面積「\(\frac{1}{8}\)」の長方形をつくり、さらにこの面積「\(\frac{1}{8}\)」の長方形を半分にすることで、面積「\(\frac{1}{16}\)」の正方形をつくることができます。

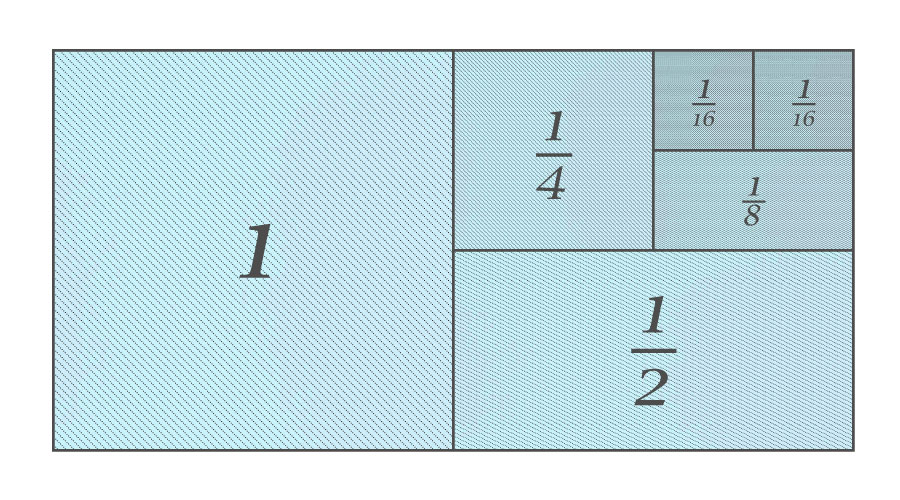
この作業を延々と繰り返していくと……

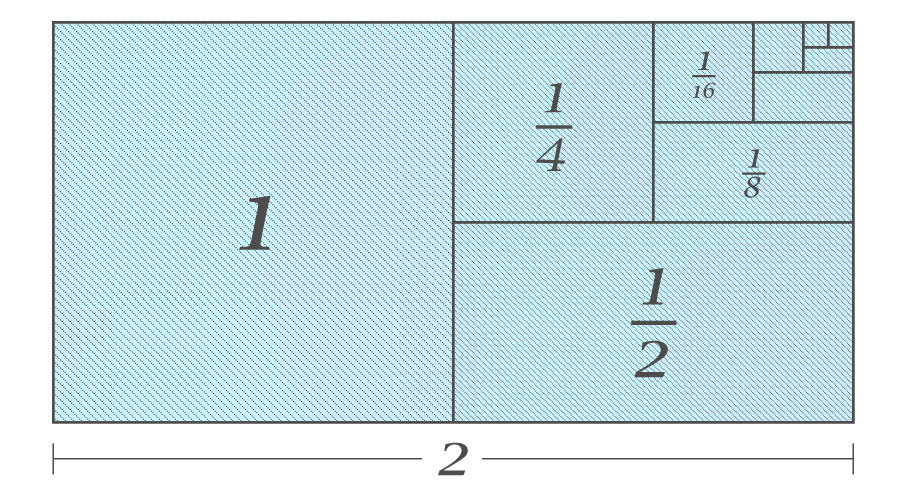
こんな風になります。

この図に出てくる長方形や正方形の面積を全て足してみると、

\[
1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}+\cdots
\]

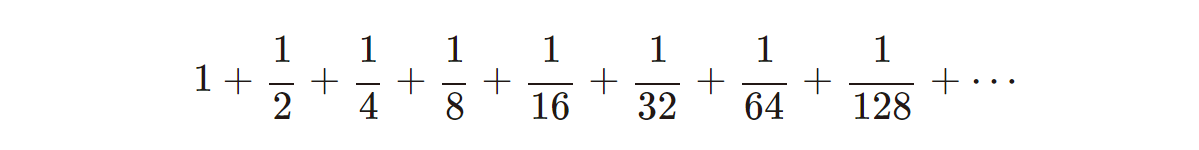
となりますよね。

そして、図に出てくる長方形や正方形は、面積「\(2\)」の長方形（面積「\(1\)」の正方形二つ）の中にキッチリと納まっています。

このようにして、図形を用いることで

\[
1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}+\cdots=2
\]

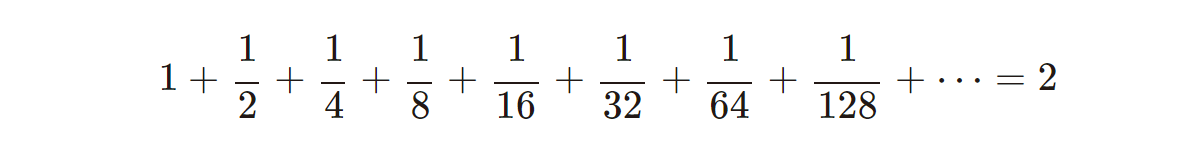
であることが納得できます。

1+1/2+1/3+1/4+1/5+1/6+⋯は何になる！？

今度は、こんな足し算を考えてみましょう。

\[
1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}+\frac{1}{9}+\frac{1}{10}+\cdots
\]

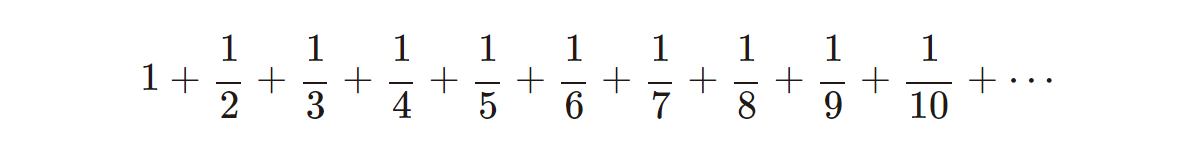
という無限に続く足し算です。

先ほどと同じように、足していく数は、徐々に小さくなっていきます。

実際に、足し算を続けて行ったら、どのような数になるか計算してみましょう。
（※\(1+\frac{1}{2}+\frac{1}{3}\)以降から、計算結果は、近似値を記載しています）

\begin{align*}
1+\frac{1}{2}&=1.5\\
1+\frac{1}{2}+\frac{1}{3}&\approx 1.8333333333333333\\
1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}&\approx 2.083333333333333\\
1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}&\approx 2.283333333333333\\
1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}&\approx 2.4499999999999997\\
1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}&\approx 2.5928571428571425\\
1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}&\approx 2.7178571428571425\\
\end{align*}

やはり先ほどのように、増加の具合は徐々に小さくなっていきますが、足し算を続けて行くので、じわりじわりと数は増え続けていきますね。

このケースは、どんどん果てしなく大きな数になっていくのでしょうか？それとも、先ほどのように、有限の値となってしまうのでしょうか？良かったら、電卓などで計算しながら予想してみてくださいね。

実は、このケースについては、どんどん果てしなく大きな数になっていくことが証明されています。

つまり、

\[
1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}+\frac{1}{9}+\frac{1}{10}+\cdots=\infty
\]

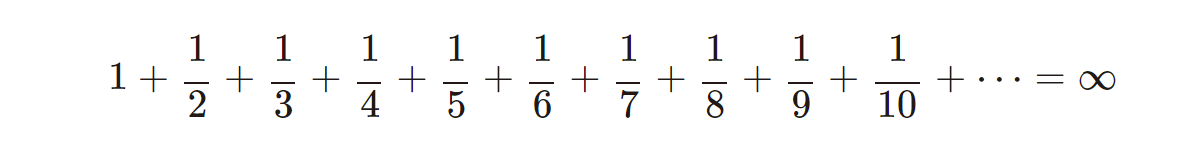
となるのです。

足していく数が、徐々に小さくなっていくからといって、必ずしも有限の値となるわけではないんですね。

無限に続く足し算の結果を予想するのは、なかなか難しそうです……。

1+1/4+1/9+1/16+1/25+1/36+⋯は何になる！？

では最後に

\[
1+\frac{1}{4}+\frac{1}{9}+\frac{1}{16}+\frac{1}{25}+\frac{1}{36}+\frac{1}{49}+\frac{1}{64}+\frac{1}{81}+\frac{1}{100}\cdots
\]

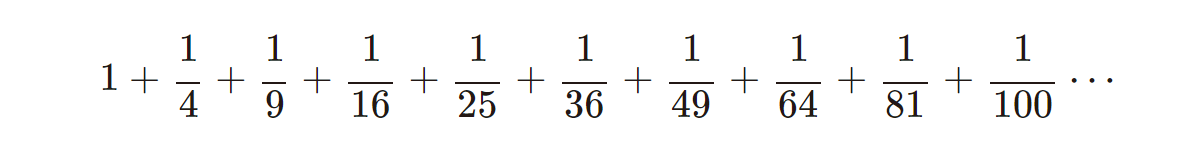
という無限に続く足し算を考えてみます。

足していく数の分母が、「\(1\times1,2\times2,3\times3,4\times4,5\times5,6\times6,\cdots\)」つまり「\(1^2,2^2,3^2,4^2,5^2,6^2,\cdots\)」となっています。このケースも、分母が大きくなっていくので、足していく数は、徐々に小さくなっていきますよね。

今回は、少しずつ足していくのではなく、プログラミングの力を使って、一気に足し算をしてみます。
（※計算結果は、近似値を記載しています）

まず100番目まで足してみると……

\[
1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\cdots\frac{1}{98^2}+\frac{1}{99^2}+\frac{1}{100^2}\approx 1.6349839001848923
\]

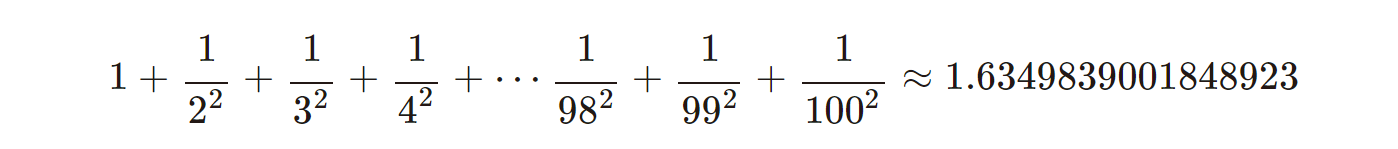
となります。

次に、1000番目まで足してみると……

\[
1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\cdots\frac{1}{998^2}+\frac{1}{999^2}+\frac{1}{1000^2} \approx 1.6439345666815615
\]

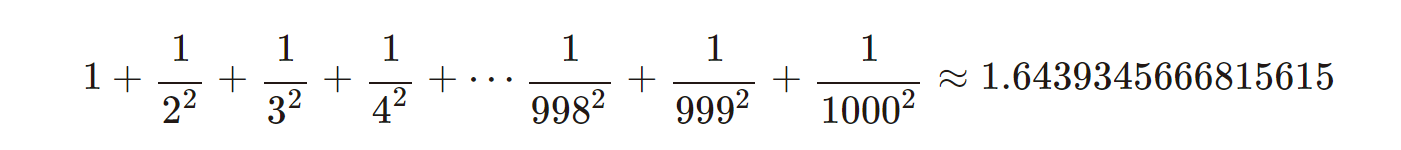
となります。

最後に、10000番目まで足してみると……

\[
1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\cdots\frac{1}{9998^2}+\frac{1}{9999^2}+\frac{1}{10000^2} \approx 1.6448340718480652
\]

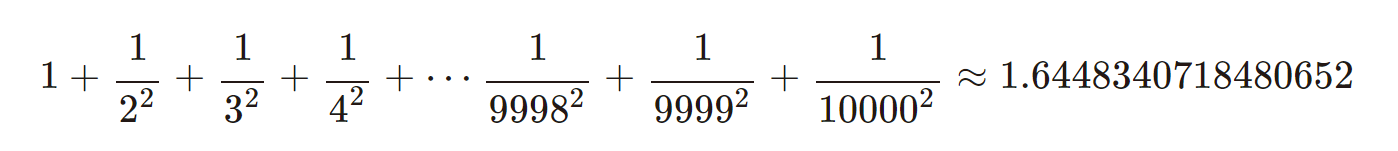
となります。

\(1.645\)くらいに近付いていっているように見えますね。

一体、この和はどんな値になっていくのでしょうか？それを知るために、今計算した三つの数それぞれを、6倍して、ルート（\(√\)）をとった値

\(\sqrt{6 \times 1.6349839001848923}\)
\(\sqrt{6 \times 1.6439345666815615}\)
\(\sqrt{6 \times 1.6448340718480652}\)

がどうなるか計算してみましょう。とても面白いことが起こります！

良かったら、電卓などで計算してみてくださいね。

結果は

\(\sqrt{6 \times 1.6349839001848923}\approx3.1320765318091053\)
\(\sqrt{6 \times 1.6439345666815615}\approx3.1406380562059946\)
\(\sqrt{6 \times 1.6448340718480652}\approx3.1414971639472147\)
（※計算結果は、近似値を記載しています）

となります。

どこかで見たことがある値に近付いているのがわかりますか？

そうです！円周率\(\pi\)です！

実は、

\[
1+\frac{1}{4}+\frac{1}{9}+\frac{1}{16}+\frac{1}{25}+\frac{1}{36}+\frac{1}{49}+\frac{1}{64}+\frac{1}{81}+\frac{1}{100}\cdots=\frac{\pi^2}{6}
\]

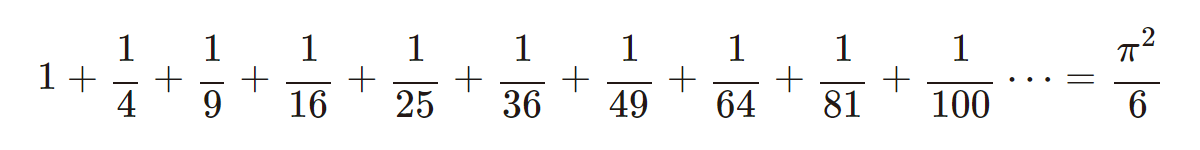
となることが証明されています。円周率が出現するなんて、驚きですね！

今回紹介した、これら三つの例は「無限級数」と呼ばれるものです。

\(∞\)になったり、有限の値になったり、突然に円周率が出てきたり……。無限級数は、私たちの直感を揺さぶり、数学の不思議さを教えてくれます。

また、今回紹介したもの以外にも、様々な面白い無限級数が存在しています。

例えば

\[
1+\frac{1}{3}+\frac{1}{9}+\frac{1}{27}+\frac{1}{81}+\frac{1}{243}+\frac{1}{729}+\cdots
\]

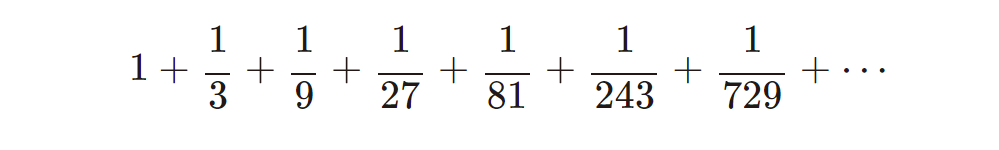
や

\[
1+\frac{1}{2^3}+\frac{1}{3^3}+\frac{1}{4^3}+\frac{1}{5^3}+\frac{1}{6^3}+\frac{1}{7^3}+\cdots
\]
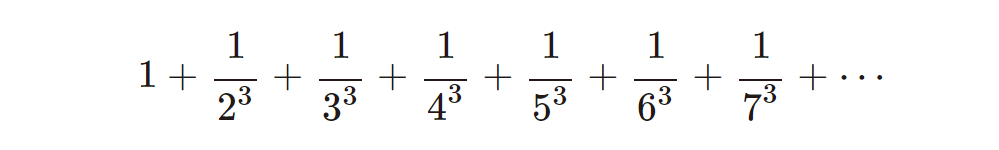
は、どうなるのでしょうか？

ぜひ電卓で計算してみたり、検索してみたりしてくださいね。無限級数の奥深い世界を楽しめるはずです！