普段、私たちが見ているこの世界。
ほんの少しだけ「数学」を知ってみると、意外な奥行きが見えてくるかもしれません。
今回、紹介するのは「春の花から見えてくる正五角形」のお話です。
道端や公園で見かける美しい花々からスタートして、数学の世界へと旅に出かけてみましょう。
春の美しい花たち
突然ですが、質問です。2021年の春は、桜を見ましたか?
新型コロナの影響で、いつも通りのお花見ができなくとも、「散歩をしながら、桜を眺めました」という人は多いのではないでしょうか。大変な時代ではありますが、やはり桜を見ると、気持ちが晴れ晴れとしますよね。

こちらの写真は、この春、私が近所を散歩していたときに撮影したものです。淡いピンクの丸っこい花びらが愛らしいですね。
そして、桜以外にも、春には色とりどりの花たちが!

ここまでに載せた2枚の写真の花たちには、ある共通点があります。
それは、どれも「花びら5枚」ということ。
この春、私は、道端で「花びら5枚の花」をたくさん見かけました。私の気のせいかもしれませんが、「花びら5枚の花」って、結構多いような気がしています。
今回は、この「花びら5枚の花」からスタートし、数学の世界を目指してみましょう!
5枚の花びらから見える図形
改めて、「花びら5枚の花」を眺めてみましょう。

5枚の花びらが、同心円状、きちんと等間隔に開いているように見えますね。
これって、よくよく考えると、ちょっと不思議なことだと思いませんか?
例えば、家族5人が、円形のテーブルに椅子を並べて座ることを想像してみましょう。

もしも、家族それぞれが、きっちり等間隔で座らなければならないとしたら、注意深く椅子を並べないといけないですよね。いい加減に椅子を並べて座ってしまうと、「3人がくっつき気味」や「1人だけ離れ気味」など、偏りが生じると思います。
しかし、今回紹介した写真の花たちの「5枚の花びら」は、偏ることなく、きちんと等間隔に開いているように見えます。まるで、分度器で測りながら、開く方向の角度を調整したかのようです。
この様子を、簡略化して、図で描いてみると……
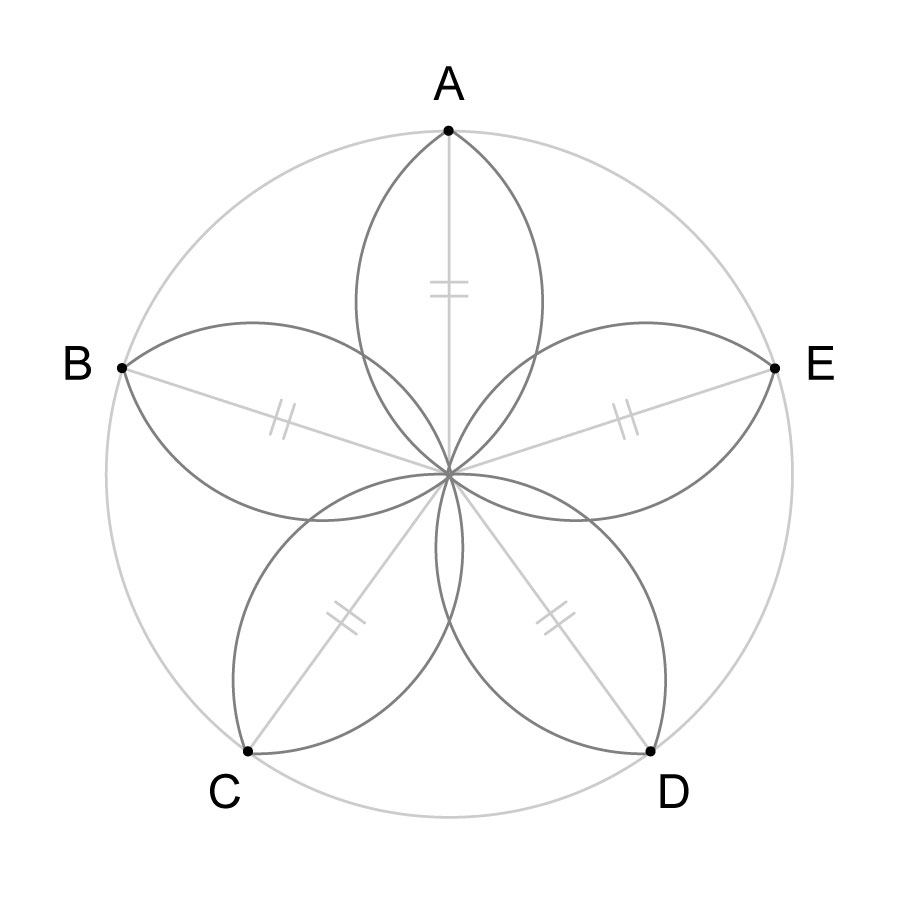
のようになります。
円を5等分しているので、真ん中の角度は、それぞれ72°です。
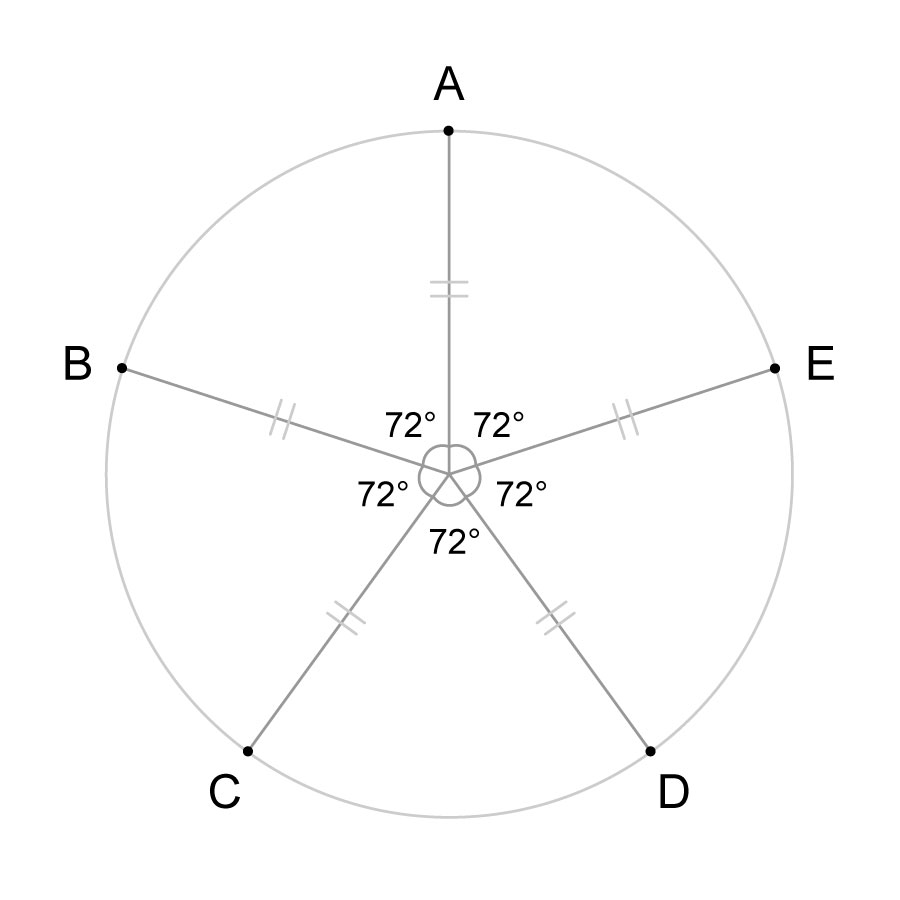
ここで、点A、B、C、D、Eを直線で繋いでみると……
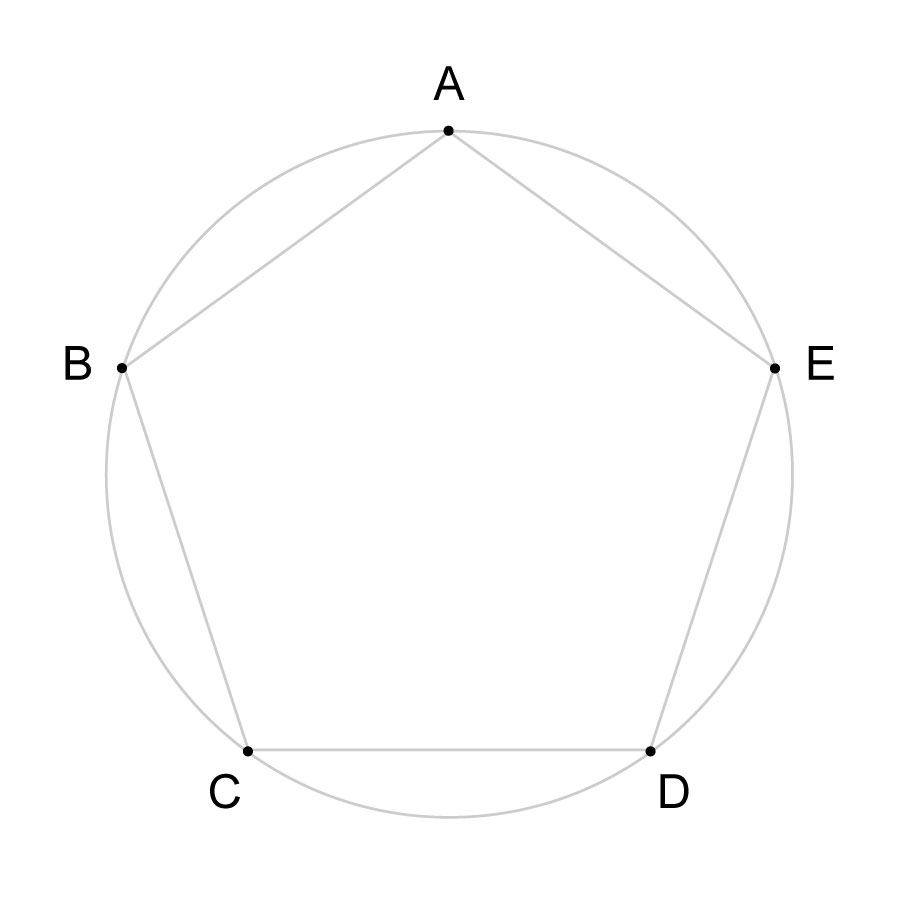
正五角形が出現しました!
では、ここからは、この正五角形について調べてみましょう。そこには「花びら5枚の花」の美しさに繋がる秘密があるかもしれません!
正五角形の対角線が織りなす形
まず、正五角形の対角線を描いてみましょう。すると……
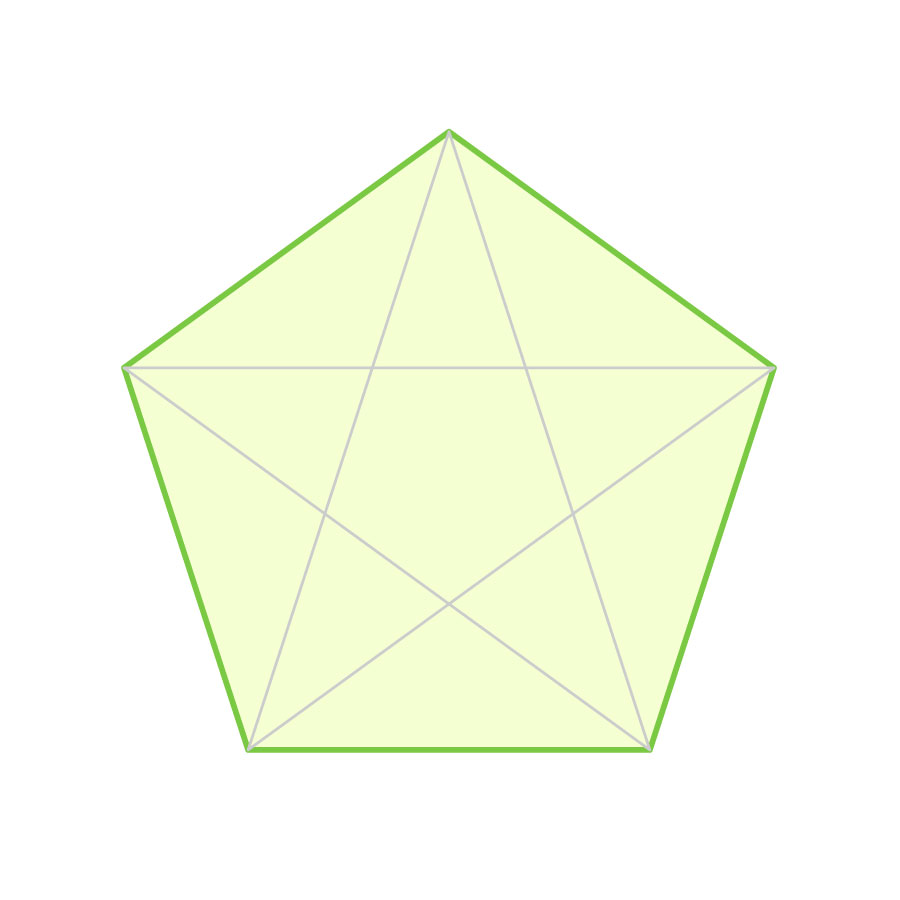
きれいな星形が出現しました!これは「五芒星」と呼ばれ、世界各所で様々な意味合いを持ちながら、用いられている形です。
例えば、京都の晴明神社の社紋は五芒星で、古くから魔除けの呪符として重宝されていたようです。海外では、モロッコなどの国旗に五芒星が使われています。

私たちの歴史から切り離せない、不思議な存在である五芒星。その面白味を数学の視点から見てみましょう。
五芒星の5本の直線は「正五角形の対角線」ですよね。ここで試しに、正六角形や正七角形の対角線も見てみることにします。

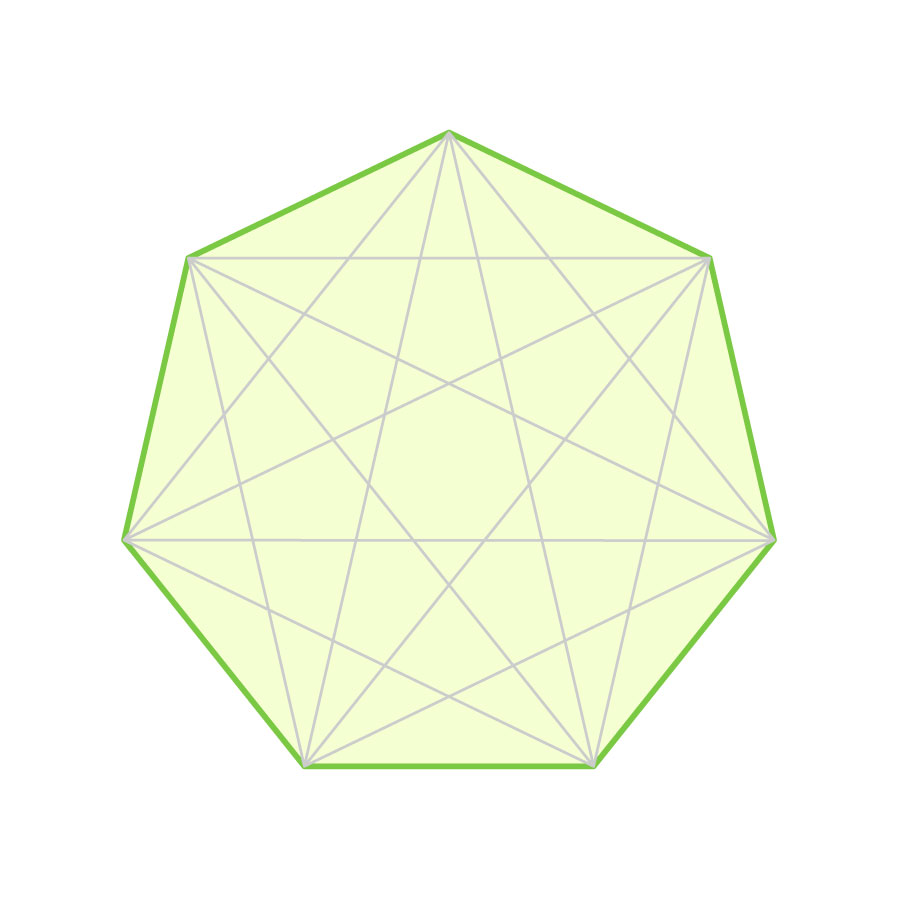
上の図の対角線の長さに注目してみてください。どちらにも、2種類の長さの対角線が存在していることがわかります。
さらに、正八角形の対角線も見てみましょう。
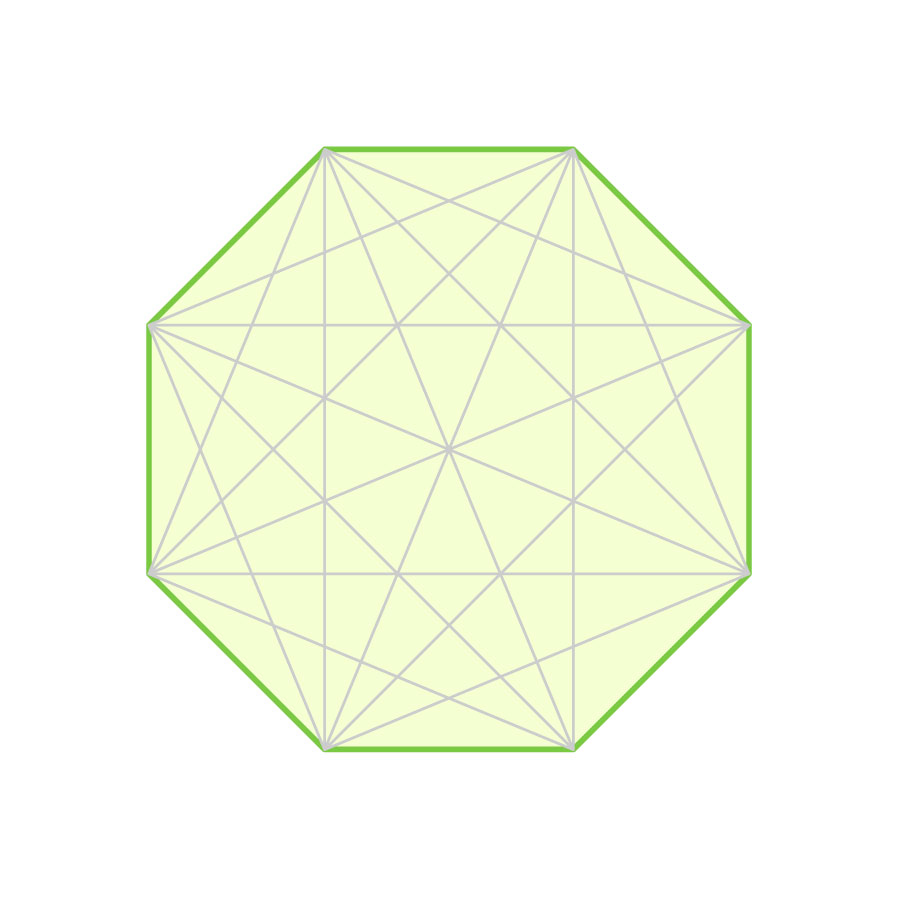
正八角形の場合は、3種類の長さの対角線が存在しています。
一方、正五角形の対角線は全て同じ長さです。実は、「全ての対角線が同じ長さ」という性質を持つ正多角形は、正方形と正五角形の2種類だけなのです。
この正五角形ならではの絶妙な均一さが、五芒星の神秘的な形状を生み出しているのかもしれませんね。
正五角形に黄金比が!?
正五角形の面白さは、これだけではありません。
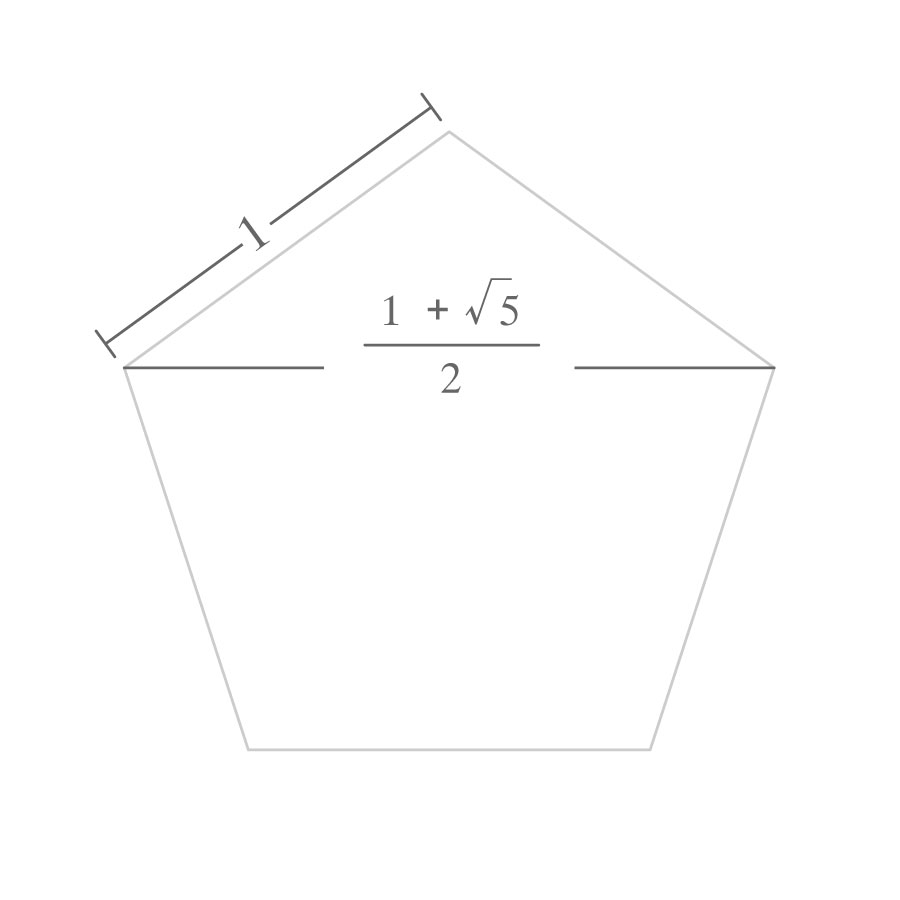
実は、正五角形の1辺の長さと、対角線の長さの比は「黄金比」と呼ばれる比になっているのです。黄金比は、古くからの建造物や美術品から見出すことができると言われている比です。
具体的な数値で言うと、正五角形の1辺の長さと、対角線の長さの比は
\[
1:\frac{1+\sqrt{5}}{2}
\]
となっています。
さらに、五芒星の中にも、黄金比が隠れているのです!
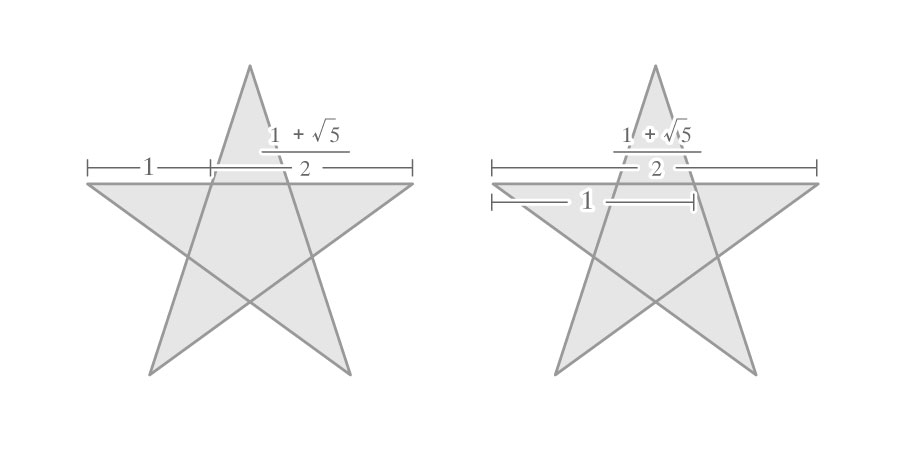
正五角形と黄金比の関係性は、なかなか深そうです……。
ちなみに、以前、黄金比に関する記事を書いたので、良かったら合わせて読んでみてくださいね。
また、上記の記事では「フィボナッチ数列」という不思議な数列を紹介しました。「5」という数は、このフィボナッチ数列に出現する数でもあります。そして、このフィボナッチ数列も、黄金比と関りが深い数列なのです。
どうやら正五角形、ただものではなさそうですね!
思い返せば、今回のスタート地点は「春の花たち」の「5枚の花びら」でした。そこから「正五角形」を見出し、「五芒星」や「黄金比」へと繋がっていきました。こんな風に思いを巡らせることで、桜をはじめとした「花びら5枚の花」の美しさの秘密に、私たちは少しだけ近づけたかもしれません。
そして、この記事を最後まで読んだあなたは、来年の桜をちょっとディープな視点で楽しめちゃうかも!?2022年は、いつも通りのお花見が楽しめると良いですね!
※Foodie https://foodie.snow.me/