普段、私たちが見ているこの世界。
ほんの少しだけ「数学」を知ってみると、意外な奥行きが見えてくるかもしれません。
みなさんが子どもの頃、近所に「駄菓子屋さん」ってありましたか?
お小遣いを握りしめて、学校帰りに友達と毎日通っていた人も多いのではないでしょうか。
そんな子どもたちの憩いの場である「駄菓子屋さん」での買い物中。実は無意識に数学的な考え方を使っていたことを知っていましたか?
それは「線形計画法」というものです。
今回は、このちょっと難しそうな「線形計画法」と「駄菓子屋さんでの買い物」に、一体どんな深い関わりがあるかを見てみましょう!
駄菓子屋さんの思い出

最近は、駄菓子屋さんが減りつつあるので、若い方の中には「あまり行ったことがない」という方もいるかもしれませんが、私自身は、子どもの頃、近所にある駄菓子屋さんへちょくちょく買い物に行っていました。今思い返すと、駄菓子屋さんは、私にとって「貴重な勉強の場」であったと思います。
「子どもだけで買い物に行かせてもらえる場所」であり、「親や先生以外の大人(店員さんやご近所さん)とのコミュニケーションの場所」であり……スーパーやコンビニとは違った経験ができる場所でした。
そして何より、駄菓子屋さんで磨かれたのは「計算スキル」!
「予算100円で、いかに好きな駄菓子を組み合わせて購入するか」というのは、子ども時代の最重要問題です。「自分なりの最高な組み合わせ」を考えながら駄菓子屋さんで悩むのは、とても楽しい時間でした。
大人にとっての100円は少額ですが、子どもにとっての100円は、駄菓子がたくさん買える大金ですよね!
あのときの「100円」を思い出しながら、色々と考えてみましょう。
予算100円!10円チョコと5円ガムを組み合わせて買おう
今、あなたは小学生だとします。お小遣い100円を握りしめ、駄菓子屋さんに来ました。
今日のお目当ては「10円のチョコと5円のガム」の2種類。この二つをうまく組み合わせて買いたいと思っています。
あなたは、チョコとガム、それぞれ何個ずつ買いますか?

これには、様々な答えがあります。
「何でもいいから、とにかく個数をたくさん買いたい!」と思ったのならば、5円ガムだけを20個購入すると良いでしょう。
「チョコが大好きなので、チョコだけを買いたい!」と思ったのならば、10円チョコだけを10個購入すると良いでしょう。
でも、それではちょっと極端かもしれません。
折角、2種類買うのですから
①できるだけバランスよく買いたい
②できるだけ多く買いたい
の両方を満たしたいところです。
……となると、何個ずつ買うのが良いでしょうか?
チョコ・ガムの組み合わせ全パターン
試しに、10円チョコと5円ガムの購入組合せを全パターン考えてみましょう。少し面倒ですが、確実な方法です。
実際に、表にしてみると以下のようになります。
| チョコの個数 | ガムの個数 | 合計 |
|---|---|---|
| 0 | 20 | 20 |
| 1 | 18 | 19 |
| 2 | 16 | 18 |
| 3 | 14 | 17 |
| 4 | 12 | 16 |
| 5 | 10 | 15 |
| 6 | 8 | 14 |
| 7 | 6 | 13 |
| 8 | 4 | 12 |
| 9 | 2 | 11 |
| 10 | 0 | 10 |
もしも「できるだけバランスよく買いたい」という気持ちを最優先するのであれば、「10円チョコ7個、5円ガム6個の合計13個」が良さそうです。
「バランスも大事だけど、できるだけ多く買いたい。チョコとガム、2個以下の差ならば許容範囲かな」と思うのならば、「10円チョコ6個、5円ガム8個の合計14個」の方が、1個多く買えるので、こちらの方が良さそうです。
少し手間はかかりますが、これで確実に「あなたにとっての最高な組み合わせ」を発見することができますね!
最適な答えを発見!「線形計画法」とは?
今回のチョコとガムのケースでは、組み合わせ方の種類が少ないため、先ほどのような「全パターン列挙」は有効な方法です。しかし、予算の金額が大きくなってしまうと、組み合わせ方の種類が増えてしまうので、「全パターン列挙」はあまり良い方法とは言えませんよね。
そんなときは、数式やグラフを使いながら、情報を整理してみることがオススメです。
今回の「予算100円で、10円チョコと5円ガムを組み合わせて購入するケース」で少し練習してみましょう。
少々難解なので、一部省略しながら解説していきます。そのため、読んでいてわからない部分があるかもしれませんが、「色んな条件を数式で表現して、考えているんだな」ということが感じられれば今回はOKです。
もしも、今回の解説をきちんと理解したい場合は、高校の数学Ⅱ「図形と方程式」を学んでみてください。
では、やってみましょう!
まず、「購入するチョコの個数」を\(x\)個、「購入するガムの個数」を\(y\)個とします。
どちらも0以上でなければならないので
\[
x\geq 0, y\geq 0
\]
という二つの不等式が成り立たなければなりません(「≥」は「≧」と同じ意味です)。
また、チョコは10円、ガムは5円なので、購入するガムとチョコの合計金額は
\[
10x+5y
\]
となります。
この合計金額は予算100円以下でなければならないので、
\[
10x+5y\leq 100
\]
という不等式が成り立たなければなりません。(「≤」は「≦」と同じ意味です)。
ここで、「チョコとガムをバランスよく買うこと」を、少し掘り下げてみましょう。
例えば、あなたが「チョコとガムの差が2個以下は許容範囲。3個以上の差は嫌だ」と感じるのであれば
\[
x-y \leq 2
\]
という不等式と
\[
y-x \leq 2
\]
という不等式が成り立たなければなりません。
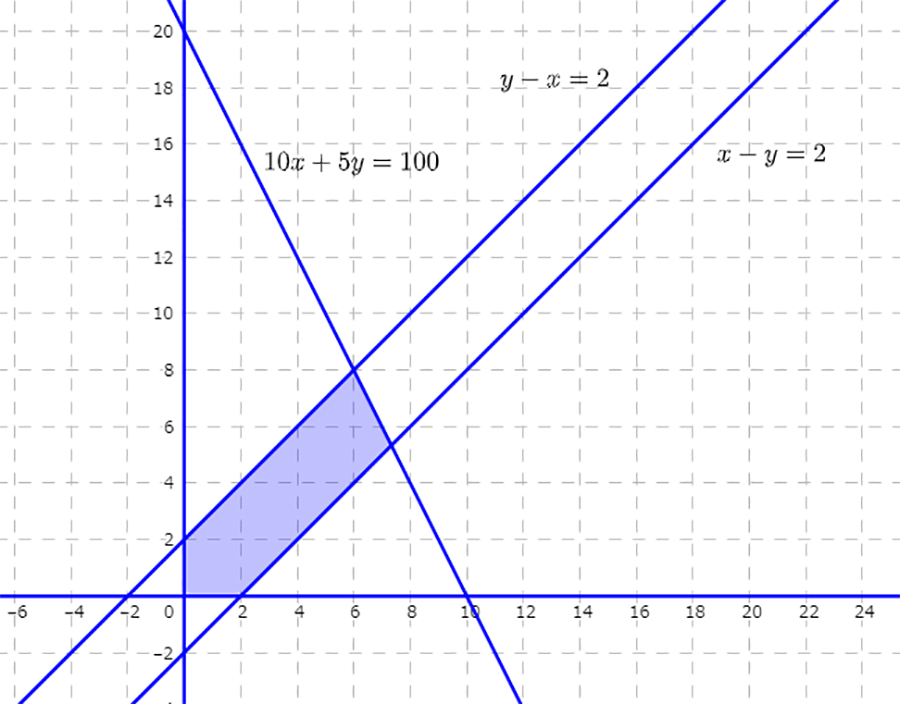
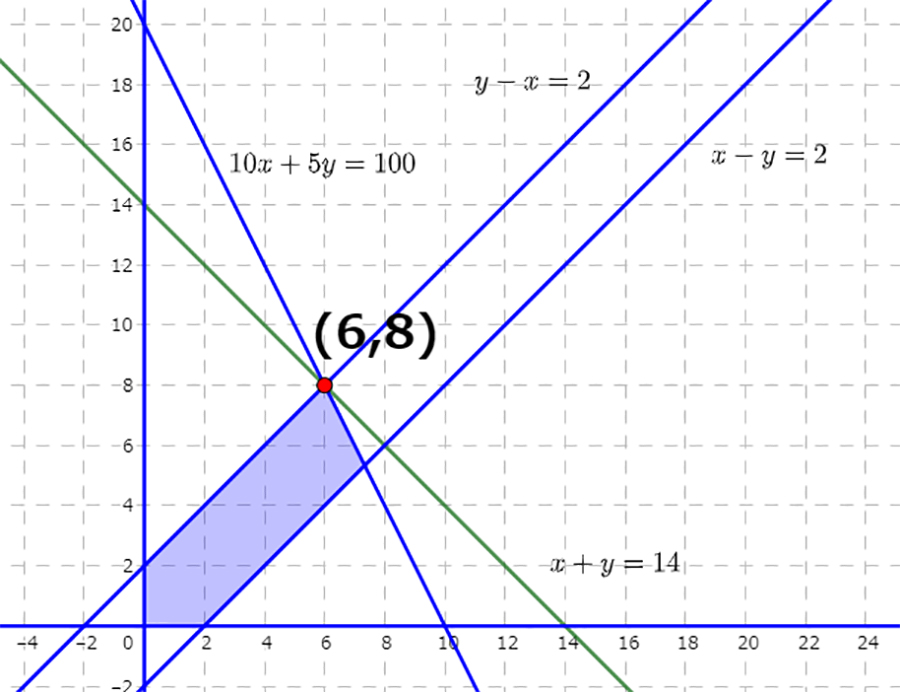
これら全ての不等式を満たす領域を、\(xy-\)平面に描いてみると、以下の塗りつぶされた部分(境界を含む)になります。
(領域の図示について詳しくは、高校の数学Ⅱ「図形と方程式」を学んでみてください)
これらの不等式で表現された条件を全て満たしながらも、できるだけ多く買いたいですよね。
この「できるだけ多く買いたい」を、数式を使って表現すると、「\(x+y\)を最大にしたい」ということになります。さらに言えば「\(x+y=k\)としたとき、\(k\)を最大にしたい」ということになります。
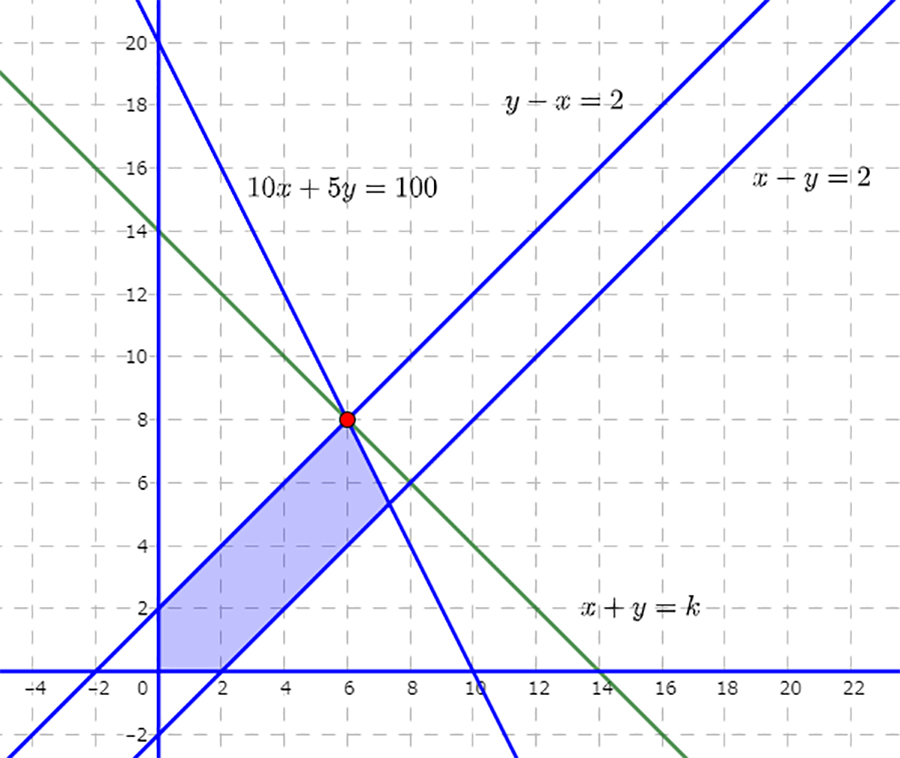
先ほどの図と合わせて、このことを考慮すると、今回のケースでは
・直線:\(10x+5y=100\)
・直線:\(y-x=2\)
という二つの直線の交点を求めれば良いことが見えてきます。
(「なぜ二つの直線の交点を求めれば良いのか?」を理解したい方は、高校の数学Ⅱ「図形と方程式」を学んでみてください)
この二つの直線の交点を求めるためには、連立方程式
\[
\begin{cases}
10x+5y=100\\
y-x=2
\end{cases}
\]
を解けば良く、実際に解いてみると
\[
x=6,\quad y=8
\]
が求まります。
つまり、「チョコ6個、ガム8個、合計14個」が求めたい答えです。
上記の連立方程式について、少し感覚的な説明をすると、「予算100円を丸々使い切りたい」を表現した数式が「\(10x+5y=100\)」で、「できるだけ多く買いたい。だから、チョコよりも安いガムをたくさん買った方が良い。でもバランスよく買いたいから、ガムとチョコの個数の差はせめて2個にしたい」を表現した数式が「\(y-x=2\)」です。
この二つをバッチリ満たす\(x\)と\(y\)を求めるために、連立方程式を解いているのです。
以上のような手法を「線形計画法」と言います。
では最後に、辞書における「線形計画法」の説明を見てみましょう。
一次の不等式または一次式で表される制約条件のもとで、一次式で表される目的関数を最大または最小にする値を求める数学的手法。生産計画・輸送計画などに応用される。リニアプログラミング。LP(linear programming)。
コトバンク「デジタル大辞泉『線形計画法』の解説」より引用(2021/5/15参照)
上記の「一次の不等式または一次式で表される制約条件のもとで」という部分は、チョコとガムの例では、「予算100円」や「チョコとガムの差は2個以下」などを不等式で表したことに対応しています。
また、「一次式で表される目的関数を最大または最小にする値を求める」という部分は、チョコとガムの例では、「購入する合計の個数(\(x+y\))を最大にする値を求める」ことに対応しています。
一見難しそうな「線形計画法」の説明でしたが、チョコとガムの例から読み解いてみると「ちょっとだけわかったかも」という気分になっているのではないでしょうか。
また、今回紹介した「線形計画法」は、駄菓子屋さんでの買い物以外にも活用することができます。
例えば「決められた予算や資源の中で、利益を最大にするための生産量は?」といったビジネスの場での問いに対しても、「線形計画法」が有効なケースがあります。
子どもの頃の駄菓子屋さんでの楽しみが、こんな便利な数学的手法に繋がっていたとは驚きですよね。そう考えると、駄菓子屋さんは、子どもたちの大切な学習の場なんだなあ、と感じます。
日本の素敵な文化「駄菓子屋さん」、これからも続いてほしいですね!
※グラフ描画サイトGeoGebra https://www.geogebra.org/