普段、私たちが見ているこの世界。
ほんの少しだけ「数学」を知ってみると、意外な奥行きが見えてくるかもしれません。
今回のテーマは「路線図」です。
駅や電車の中で、見かける「路線図」。私たちにとって、とても身近な存在ではありますが、そこには、ある数学の一分野が隠されているのです。
とても便利な「電車の路線図」
あなたは最近、電車の路線図を目にしましたか?
今はスマホで乗り換え案内を簡単に調べられるので、「あまり見なくなったな」という人もいるかもしれませんね。
しかし、旅行先などの土地勘のない場所へ訪れたとき、かなり丁寧に路線図をチェックした経験がある方は多いのではないでしょうか。
路線図の便利な点を挙げてみると
・現在地と目的地の大まかな位置関係がわかる
・現在地から目的地までの停車駅の数がわかる
・乗り換える駅がわかる
など、色々ありますよね。
路線図を見ながら「乗り換え少な目で行くなら、このルートかな」や「東京駅を経由したいから、少し遠回りだけど、このルートにしよう」など、目的に応じて、様々なことを考えることができます。
そんな、とても便利な路線図。しかし、よくよく見てみると、ちょっと不思議なところがあるのです。
それを「山手線の路線図」を観察しなから、探ってみましょう!
山手線は丸くない!?
「山手線の路線図」と聞くと、きれいな円形のものを思い浮かべる方が多いのではないでしょうか。
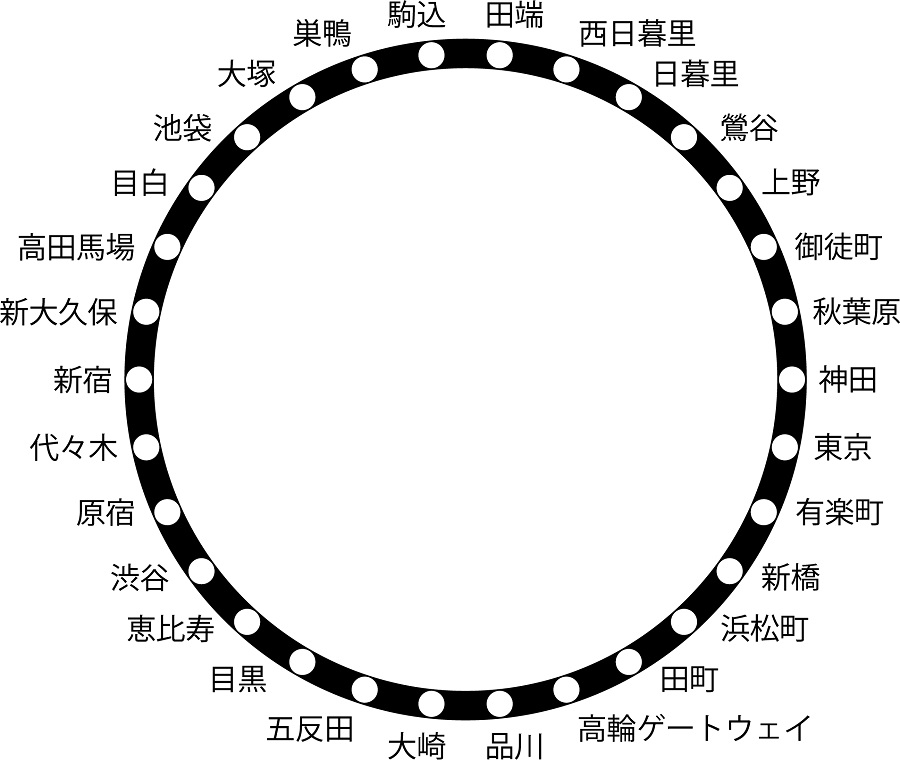
丸く1周つながった形状を見ることで「山手線にずっと乗り続けていると、元来た位置に戻る」ということがよくわかりますよね。
そして、たとえ山手線で寝過ごしたとしても、東京23区内を出ることがないということもよくわかります。東海道線の場合は、東京駅から出発して、横浜駅で降りようと思っていたら寝過ごしてしまい、熱海駅まで行ってしまった……という悲劇もあり得ますよね。
このように、シンプルな円形の路線図から、私たちは「山手線」に関する様々な情報を受け取ることができるのです。
しかし、ちょっと待ってください!
「山手線の本当の路線」って、こんなにきれいな円形なのでしょうか?きっと、そんなはずないですよね。
実際に「山手線の本当の路線」に近い形で、路線図を描いてみると、以下のようになるようです。
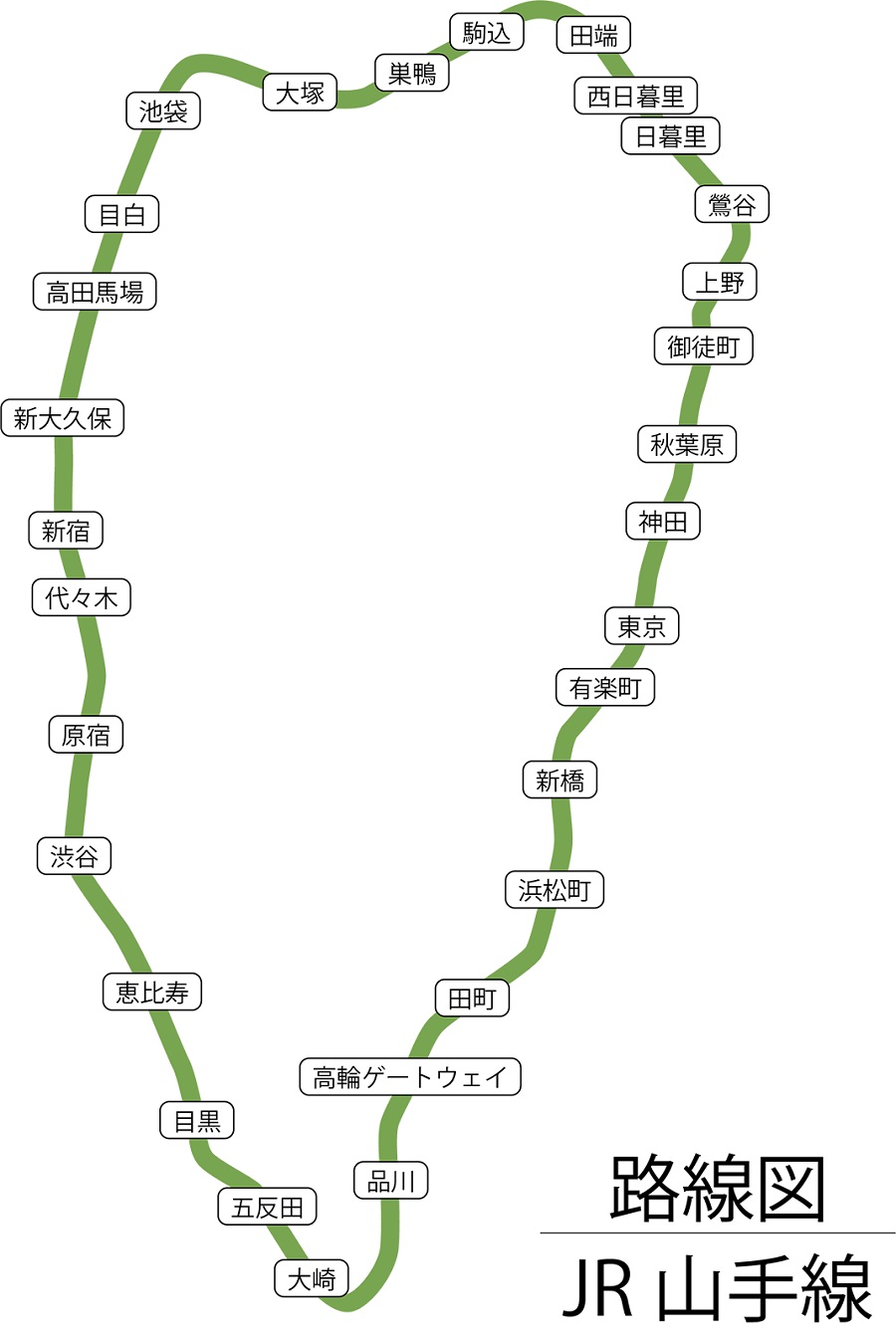
縦長ですし、グネグネ蛇行していて、先ほど見た「きれいな円形の山手線の路線図」とはかなり違う形状です。
しかし、私たちは「きれいな円形の山手線の路線図」と「縦長でグネグネ蛇行した山手線の本当の路線」を、当たり前のように「同じもの」と見なして、路線図を活用しています。
形状は全く違うのに「同じもの」って……よくよく考えると、これって不思議な見方だと思いませんか?
例えば、△と○を見て、これらを「同じもの」と思う人はなかなかいませんよね。
一体、「山手線の路線図」には何が起こっているのでしょうか?
路線図のポイントは「つながり方」
「きれいな円形の山手線の路線図の形状」は「縦長でグネグネ蛇行した山手線の本当の路線の形状」を変形することで、出来上がります。
かなり大胆な変形をしているように見えますが、「好き勝手に形状を変えても良い」というわけではなく、注意点があります。
特に「形状を変形するときに、実際の路線のつながり方を変えないこと」は、とても大切な注意点です。
例えば、東京駅~熱海駅までを表す東海道線の路線図を、山手線のように円形にしていい……なんてことはありませんよね。東京駅と熱海駅をつなぐことで、円形の路線図にしてしまったら、それを見た人が「熱海駅と東京駅は隣同士なんだ」「東海道線に乗り続けていると、1周回って元いた位置に戻るんだ」と誤解してしまいます。
また、複数の路線が描かれている路線図が、実際の路線とは全く異なった「つながり方」になっている場合、乗り換える駅などを正確に把握することができなくなってしまいます。
こんな風に「つながり方が、実際の路線と全く違う路線図」では、路線図本来の目的を果たせません。

路線図を描くときは「つながり方を変えないこと」が、とても大切なポイントなんですね!
グニャグニャと変形する数学の分野「トポロジー」とは?
路線図では「つながり方を変えずに形状を変形する」ということをしていました。実は、これには、ある数学の分野が関わっています。
それは「トポロジー」という幾何学の一分野です。日本語では「位相幾何学」と言います。
私たちが小中高のときに学んだ幾何学では、「角度を求めましょう」「長さを求めましょう」といった問題をたくさん解きましたよね。角度・長さ・面積・比などを求め、正確な形状を把握することが大切でした。
しかし、同じ幾何学でもトポロジーでは、かなり違った見方をします。
そんなトポロジー特有のちょっと不思議な幾何学の世界を体験してみましょう!
まず、グニャグニャと伸縮自在なゴムのような素材の紐を思い浮かべてみてください。その紐がアルファベットの「O」のような輪っかの形になっているとします。
この紐を、うまく変形することで、アルファベットの「D」の形をつくることができますよね。また、逆に、「D」の形になっている紐を「O」の形に変形することも可能です。
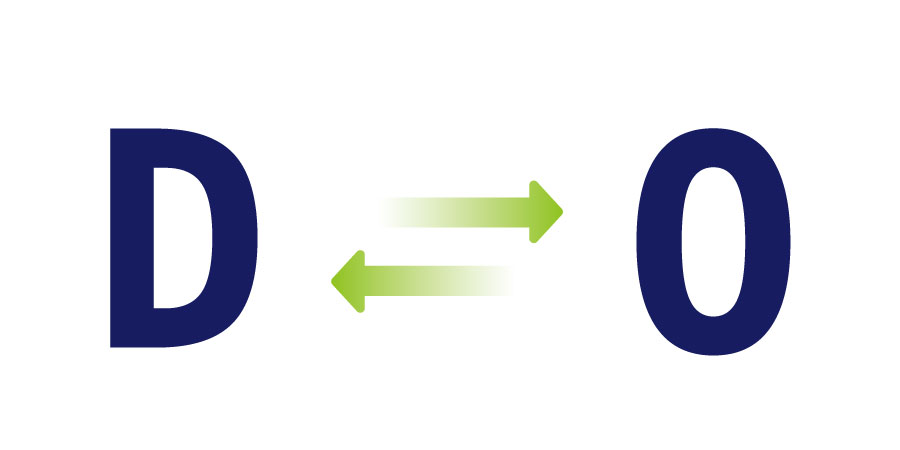
トポロジーでは、これら「O」と「D」は「同じもの」であると考えます(正確には、「位相同型」や「同相」と言います)。
そして、OとDは、見た目の形状は違うものの、「つながり方」は同じです。どちらも、山手線のように、1周まわると元の所へ戻る形状です。
次に、アルファベットの「T」の形の紐を思い浮かべてみてください。
「T」の上の部分の両端を、斜め上方向へ伸ばすことで、アルファベットの「Y」の形をつくることができますよね。また、逆に、「Y」の形になっている紐を「T」の形に変形することも可能です。

トポロジーでは、これら「T」と「Y」も「同じもの」であると考えます。この二つも見た目の形状は違うものの、「つながり方」は同じです。分岐点(下図のX)が一つあり、そこから三方向(下図のA,B,C)へ進むことができます。
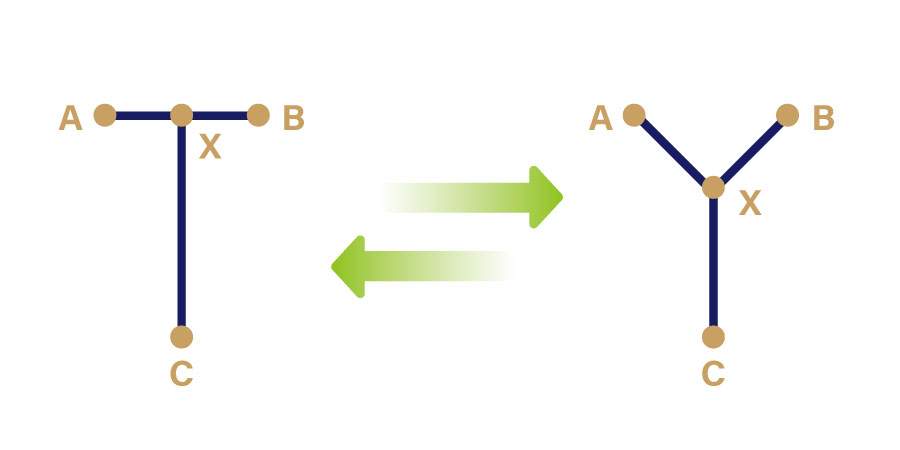
このように、トポロジーでは「グニャグニャと連続的に変形しても『変わらない性質』に注目する」ということをしていきます。
こんな風に、ちょっと不思議な見方をするせいか「トポロジーの研究者は、コーヒーカップとドーナツを区別できない」なんて言われることもあるのです。
なぜならば、コーヒーカップが粘土のようにグニャグニャした素材でできていたとしたら、ドーナツの形状に変形することができてしまうからです。

どちらも全く違う形状ではありますが、コーヒーカップの持ち手の「穴」と、ドーナツの真ん中の「穴」が対応し、どちらも「穴が一つ」という重要な共通点を持っているのです。

「コーヒーカップとドーナツは同じもの」なんて言うと、かなり不思議な分野に感じるかもしれませんが、私たちは路線図を見るときに、トポロジーの考え方を使っています。
もしも「縦長でグネグネ蛇行した山手線の本当の路線」が、伸縮自在なゴム紐でできていたとしたら、それをグニャグニャと変形して「きれいな円形」にすることが可能です。このようにして、「つながり方」を変えることなく、シンプルで見やすい「きれいな円形の山手線の路線図」ができあがります。
そして、私たちは「きれいな円形の山手線の路線図」と「縦長でグネグネ蛇行した山手線の本当の路線」を「同じもの」と見なしながら、路線図を利用しています。これって、まさにトポロジーの考え方ですよね。
このように考えてみると、「トポロジーって不思議なように見えて、案外身近なんだな」と感じられるのではないでしょうか。
そして、路線図以外にも、トポロジーのような考え方を使っている場面は、意外なところに潜んでいるかもしれません。
例えば、プレゼン資料などで、「関連性を示す図」を描くときに、つながり方は変えず、形状を見やすいように変形する……というのも、その一つだと思います。下の写真の左上にある「User-Centered Design」の資料も、そんなことに配慮しながら作られたのかもしれません。

あなたの身の回りにある「トポロジー」、ぜひ探してみて下さいね。今までとは違った世界が見えてくるかも……?
※参考文献
●Richard Earl「Topology: A Very Short Introduction (Very Short Introductions)」(OXFORD UNIVERSITY PRESS)
●夢ナビ「コーヒーカップとドーナツは同じ形? 『トポロジー』で考える世界」(2021/6/13参照)
https://yumenavi.info/lecture.aspx?GNKCD=g005991