普段、私たちが見ているこの世界。
ほんの少しだけ「数学」を知ってみると、意外な奥行きが見えてくるかもしれません。
今回のテーマは、私たちの生活に欠かせない「お金」にまつわる数学です。
ローン、預金、資産運用……大人になると、誰もが考えなければならないお金の話。そのなかでも、今回は「利息」について、考えていきましょう。
借金が雪だるま式に増える
「借金が雪だるま式に増える」という言葉がありますよね。

雪だるまをつくるとき、まずは手で固めて小さな雪玉をつくり、それを転がしながら、雪を付着させていき、雪玉を大きくしていきます。
雪玉は転がすごとに、どんどん大きくなっていくので、「最初はあんなに小さい雪玉だったのに!」と驚きますよね。
そんな風に、借金も大きくなっていく……という意味が「借金が雪だるま式に増える」という言葉に込められています。
では、この「雪だるま式」の様子を、数学の視点から探っていきましょう。
1000円だけ借りたはずなのに……!?
まずは、架空のお話を紹介します。
ある日、太郎さんは、昼食代が足りなかったので、次郎さんに「1000円、貸して」とお願いしました。
すると、次郎さんは「いいよ。でも、1ヶ月経つごとに、1割増やして返してほしい。1ヶ月後に返すならば、1000円を1割増やして、1100円。2ヶ月後に返すならば、1100円を1割増やして、1210円。3ヶ月後に返すならば、1210円を1割増やして、1331円ね」と言いました。
太郎さんは、この提案を受け入れて、次郎さんから1000円を借りることに。返済が遅れても、数百円多く支払うだけならば、問題ないと考えたのです。
少額の借金だったため、太郎さんは、借金のことをすっかり忘れ、返済することなく月日が過ぎていきました。
そして、12ヶ月後。次郎さんは、太郎さんに「あのときの借金返してよ」と言いました。
太郎さんは「いいよ。いくらになってる?」と聞いたところ、次郎さんは「小数点以下切り捨てで、3138円」と告げたのです。
なんと、借金は3倍以上に!太郎さんは、次郎さんに騙されているのでしょうか?

確認するために、次郎さんへの返済額を計算してみましょう。
1ヶ月後:\(1000\times 1.1=1100\)
2ヶ月後:\(1100\times 1.1=1210\)
3ヶ月後:\(1210\times 1.1=1331\)
4ヶ月後:\(1331\times 1.1=1464.1\)
となっていくので、1.1を掛け算していくことで、計算できます。
この計算をくりかえして、表にしてみると……
| 0ヶ月後 | 1000 |
| 1ヶ月後 | 1100 |
| 2ヶ月後 | 1210 |
| 3ヶ月後 | 1331 |
| 4ヶ月後 | 1464 |
| 5ヶ月後 | 1610 |
| 6ヶ月後 | 1771 |
| 7ヶ月後 | 1948 |
| 8ヶ月後 | 2143 |
| 9ヶ月後 | 2357 |
| 10ヶ月後 | 2593 |
| 11ヶ月後 | 2853 |
| 12ヶ月後 | 3138 |
(小数点以下は切り捨て)
確かに、12ヶ月後には3138円となっているのです。
0ヶ月後と1ヶ月後、1ヶ月後と2ヶ月後、2ヶ月後と3ヶ月後の差額は、それぞれ100円、110円、121円ですが、10ヶ月後と11ヶ月後、11ヶ月後と12ヶ月後の差額は、それぞれ260円、285円となっていますね。
返済額は、じわじわと加速しながら増えていくことがわかります。
もっと先まで考えてみましょう。
2年後、つまり、24ヶ月後の返済額は、9849円(小数点以下切り捨て)となり、約10倍の額となります。
5年後、つまり、60ヶ月後の返済額は、30万4481円(小数点以下切り捨て)となり、300倍以上の額となります。
10年後、つまり、120ヶ月後の返済額は……なんと9200万円以上となるのです!
最初は1000円で、増え方も数百円単位だったのに、こんなにも大きくなるなんて驚きですよね。
今回のケースのように、前の期間の利息を繰り入れて、次の期間の新元金として計算していく方法は「複利法」と呼ばれています。
0ヶ月後から1ヶ月後は元金1000円だけに対する利息を考えていましたが、1ヶ月後から2ヶ月後は1100円、つまり、「元金1000円+利息100円」を新元金として、これの1.1倍を計算することで、1210円としていましたよね。
そして、先ほど計算した通り、複利法を用いると、最初の利息が少額だったとしても、年月を追うごとに、加速しながらどんどん大きくなっていくのです。
そのため、短期的だけでなく、「長期的にどうなるか?」もしっかり確認しておく必要があるんですね。
今回は借金をテーマにしましたが、資産運用でも、同様の計算をすることがあります。来年、再来年だけでなく、数十年後のこともよくよく考えて、計算しなければならないことがわかりますね。
※次郎さんのような行為を、真似することはやめましょう。違法行為に該当する可能性があります。
複利法と数学
実は、この複利法は、数学の重要なトピックと関わっています。
そのことを確認するために、もう一つ、架空のお話を紹介します。
次のお話は、お金に関することではなく、「招待制SNS」がテーマです。複利法とは関係なさそうに見えますが、一体どんなつながりがあるのでしょうか?

とある招待制SNSがリリースされたとします。
このSNSは、「1人のSNSユーザーが、新規に3人の友人を招待できる」というもの。
まずは、SNS運営者の1人が、3人を招待しました。これを第1段階としましょう。
そして、その3人もそれぞれ、3人を招待すると、9人を新規に招待したことになります。これを第2段階としましょう。
さらに、その9人もそれぞれ、3人を招待すると、27人を新規に招待したことになります。これを第3段階としましょう。
このように、「招待された人が、新規に3人招待すること」を繰り返していった場合、どのようになっていくのでしょうか?
まずは、第10段階までの新規SNSユーザーを計算してみましょう。3を掛け続けていけば良いので、以下のようになります。
| 第1段階 | 3 |
| 第2段階 | 9 |
| 第3段階 | 27 |
| 第4段階 | 81 |
| 第5段階 | 243 |
| 第6段階 | 729 |
| 第7段階 | 2187 |
| 第8段階 | 6561 |
| 第9段階 | 19683 |
| 第10段階 | 59049 |
ここまででも、かなり大きな数になりました。
「1人から始めて、3人しか招待できない」というルールだったのに、意外なほど増えていきますね。
さらに先まで計算してみましょう。
第15段階までいくと、1434万8907人となります。
第16段階までいくと、4304万6721人となります。
第17段階までいくと、1億2914万163人となります。日本の人口くらいの人数になりました。
そして、第20段階までいくと……34億8678万4401人となるのです!
あっという間に、とんでもない人数になってしまいました。
このように、1より大きい一定の数を掛け算し続けていくと、想像以上にどんどん大きな数になっていくのです。
このことを、数学では「指数関数的な増え方」などと表現します。
先ほどの借金の例でも、1.1を掛け続けていましたよね。つまり、複利法も「指数関数的な増え方」をするものの一例なのです。
では、指数関数とはどのようなものなのか、見ていきましょう。
まず、招待制SNSの例を数式にしてみると、第\(x\)段階の新規SNSユーザーを\(y\)人としたとき
\[
y=3^x
\]
となります。
数式にすると、一見難しそうに見えますが、
第1段階:\(y=3^1=3\)
第2段階:\(y=3^2=3\times 3=9\)
第3段階:\(y=3^3=3\times 3\times 3=27\)
のように、具体例を計算してみると、納得いくと思います。
現状では、この\(x\)には、\(1,2,3,4,\cdots\)のような正の整数と呼ばれる数のみを代入していますが、代入できる数の範囲を、実数と呼ばれる数にまで拡張することができます。
実数は、「数直線上の数」に対応しており、小中学校で学ぶ、ありとあらゆる数が実数に含まれています。例えば、\(1.25\)などの小数や、円周率\(\pi\)も、実数です。
\(3^x\)の\(x\)に代入する数を、正の整数だけでなく、実数へと広げることが可能なので、例えば、\(3^{1.25}\)や\(3^{\pi}\)の値も考えることができるようになります。
「どのように実数へ拡張するのか?」については、高校で学ぶ数学Ⅱのテキストなどを参照してみてくださいね。
そして、\(x\)に実数を入れることができるようになった
\[
y=3^x
\]
という関数は、「3を底(てい)とする指数関数」と呼ばれています。
では、この関数のグラフを描いて、増え方の様子を見てみましょう。
原点付近では
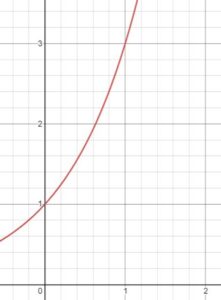
built by Desmos
となっていて、比較的なだらかな増え方に見えます。
しかし、縮尺を変えて、広い範囲でグラフを見てみると……
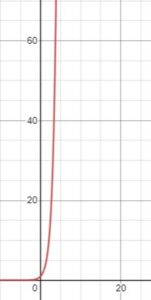
built by Desmos
急激に増えていく様子がわかりますね!
このように、「指数関数的な増え方」では、最初のうちは小さな増え方に見えても、どんどん加速していき、あっという間に驚くほど大きくなってしまう性質があるのです。
借金の例も数式にしてみると、\(x\)ヶ月後の返済額を\(y\)円としたとき
\[
y=1000 \times {1.1}^x
\]
となります。これも、\(x\)に代入できる数を実数へと拡張すれば、\({1.1}^x\)という部分が「1.1を底(てい)とする指数関数」なので、\(3^x\)の場合と同様に、「指数関数的な増え方」をしていきます。
今回挙げた2つの例では、1.1を掛けたり、3を掛けたりと、「1より大きい一定の数を掛け算し続けていく」という、とてもシンプルな計算をしていただけなのですが、その増え方は凄まじいものでした。
理系の人は、このような様子を「発散スピードが速い」といった表現することがあります。ざっくり言うと、「正の無限大へ向かうスピードが速い」という意味です。\(y=2x\)などの一次関数をグラフ化した右肩上がりの直線も、正の無限大に向かっていきますが、その速度は、指数関数には全く及びません。それほどまでに、指数関数は圧倒的なのです。
このように考えると、なかなか恐ろしいものですが、複利法はじめ、私たちの身の回りには「指数関数」が、さりげなく潜んでいます。
もしも、日常のなかで「1より大きい一定の数を掛け算し続けていく計算」を見つけたときは、電卓などで計算しながら、その行く先を注視してみると良いかもしれません。
【記事内のグラフ描画に使用したサイト】
Desmos https://www.desmos.com/calculator?lang=ja