普段、私たちが見ているこの世界。
ほんの少しだけ「数学」を知ってみると、意外な奥行きが見えてくるかもしれません。

今回のテーマは「刺繍」です。

刺繍と聞くと「家庭科で習うものなのに、数学と関係があるの？」と思う人もいるかもしれません。しかし、実は、ある視点から見ると、とても深く関わり合っているのです。

刺繍の面白さとは？

服や雑貨などに施された刺繍を見て「素敵！」と感じたことはありませんか？

針と糸が織りなす刺繍の精巧さ、美しさ、ユニークさに驚いた経験がある人は多いと思います。

私自身は不器用なので、刺繍をすることは、ほとんどありません。しかし、初めて刺繍にチャレンジした家庭科の授業のことは鮮明に覚えています。

下手ながらも「針と糸で絵が描ける！」と嬉しくなったのです。

バックステッチという技法を使って、数ミリ単位の細かな縫い目を重ねていくことで、徐々に図柄が浮かび上がってくる……というのは、なかなか楽しい時間でした。

特に面白味を感じたのは「縫い目一つ一つは直線なのに、すごく細かくすると、丸みのあるカーブも描ける」ということ。

縫い目を細かくするほど、カーブがより精密に表現されるので、「不器用だけど、できるだけ丁寧に縫おう！」と意気込んだものでした。

「直線から、直線でないものが生み出されていくこと」は、当時の私にとって、不思議に感じる体験だったのです。

【※注意】実際には、数学用語としての「直線」とは、端点を持たず、まっすぐ無限にのびる線のことで、有限の長さで区切られたものは「線分」と呼びます。本記事では、日常用語にならって、単に「まっすぐな線」という意味で「直線」という言葉を使っていきます。

直線だけなのに、丸い！？

刺繍のように、「細かな直線で、丸みのある曲線を表現する」という考え方は、数学において非常に重要なものです。

円をテーマに、その様子を体験してみましょう！

まず、正六角形や正八角形を想像してみてください。

カクカクした形状が思い浮かんだと思います。

しかし、正30角形や正40角形にしてみると、その様子は変わっていくのです。

まず、正30角形の形状を見てみましょう。

少しカクカクしていますが、遠目で見たら「ほぼ円」ですよね。

次に、正40角形の形状を見てみましょう。

かなり近付いて見ると、カクカクしていることがわかりますが、肉眼では「これは円と言っても良いだろう」というくらい丸みを帯びています。

本当は一つ一つ直線のはずなのに、ほとんど円に見えるなんて、ちょっと不思議ですよね。まさに刺繍のようです。

なぜ円周率は3より大きいの？　～円周率とは？～

では、ここまでの話をヒントに「なぜ円周率は3より大きいか？」を探ってみましょう。

まず、その前に「円周率とは何か」を知っておく必要があります。3.14で有名な円周率ですが、その定義をご存知ですか？

円周率とは「円の直径と円周の長さの比」です。

円の半径を\(r\)、円周の長さを\(l\)とすると、円周率\(\pi\)は
\[
\pi = \frac{l}{2r}
\]
と表されます。つまり、「円周率=円周/直径」ということです。

分母を払うと
\[
l=2r\times \pi
\]
となり、「円周=直径×円周率」という、よく知られている公式が出てきました。

特に、直径1、つまり、半径\(\frac{1}{2}\)の円については
\[
l= \pi
\]
となるので、「円周=円周率」が成り立っています。

つまり、直径1の円の円周を求めれば、円周率が求まるのです。

「円周を求めればいいから、直径×円周率を計算すればいいんだ！円周率は3.14だから、1×3.14だな」と思った方、ちょっとお待ちください。

円周率の定義からスタートして、「円周率の値は3より大きい」を導こうとしているのに、近似値3.14を使ってしまっています。

これでは、「今からカレーの作り方を説明します。ここに完成品のカレーがあります。はい、できました！」と言っているようなものです。

今は、近似値を求める道の途中。その道を少しずつ進んでいく必要があります。

一体、どのように直径1の円の円周を求めるのでしょうか？

丸みを帯びた形状の長さを測るためには……と考えてみると、刺繍がヒントになってきます。

なぜ円周率は3より大きいの？　～正多角形による近似～

ここで使うのが、「正多角形で近似していく方法」です。

まず、直径1の円の上に、等間隔で6つの点を打ちます。

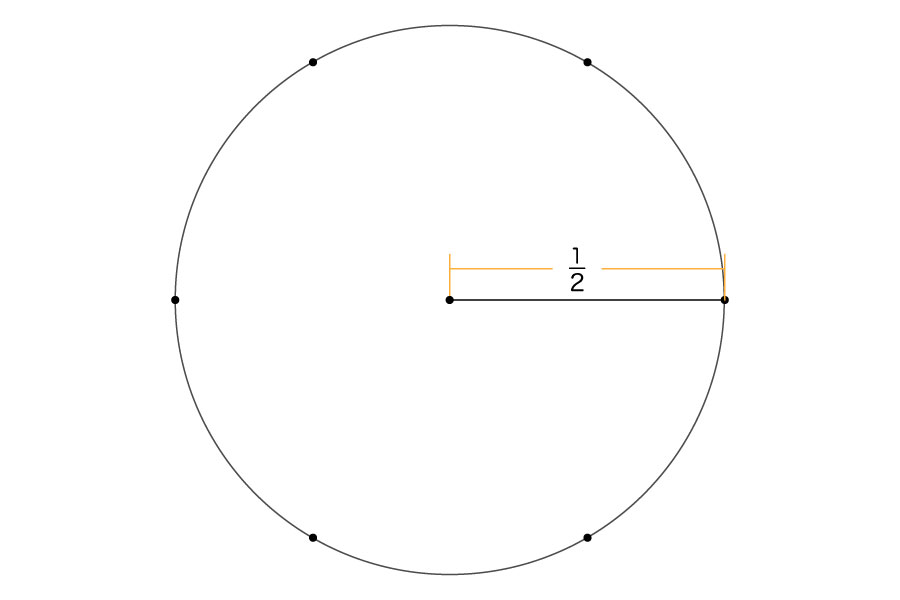
そして、この6点を、縫い目のように直線でつないでいくことで、正六角形ができあがります。

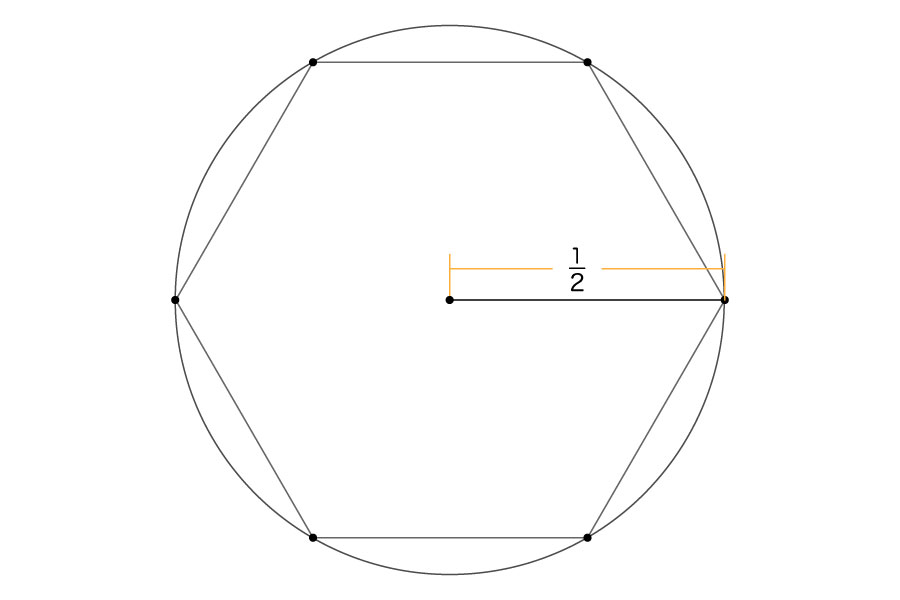
円周は、この正六角形一周の長さよりも大きいですよね。つまり

円周 ＞ 正六角形一周の長さ

となっています。そして、正六角形一周の長さは、正六角形の1辺の長さ6つ分なので

円周 ＞ 正六角形の1辺の長さ×6

ということになります。

では、正六角形の1辺の長さを求めていきましょう！

円の中心から、放射状に正六角形を6等分すると、以下のように6つの三角形が出現します。

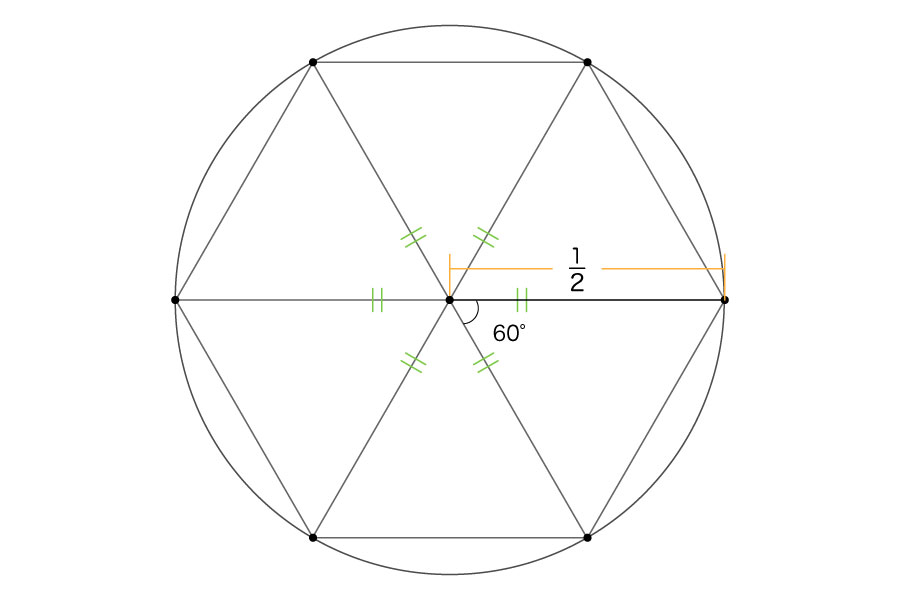
この6つの三角形は、2つの辺が円の半径\(\frac{1}{2}\)となっている、二等辺三角形です。そして、その2辺に挟まれる角の大きさは、360°を6等分したものなので、60°となっています。

二等辺三角形なので、残り2つの角度は同じ大きさになりますよね。三角形の内角の和は180°であることを使って、残りの角度を求めてみると……
\[
\frac{180-60}{2}=\frac{120}{2}=60
\]
となり、60°であることがわかります。

つまり、6つの三角形は、全て正三角形。ということは、これらの三角形の辺の長さはすべて同じだったのです。

このことから、正六角形の1辺の長さは\(\frac{1}{2}\)であることがわかります。

これを

円周 ＞ 正六角形の1辺の長さ×6

に当てはめてみると……

円周 ＞ 3

となりますね。

そして、先ほど説明したように、直径1の円の場合は「円周=円周率」となっているので

円周率 ＞ 3

が導き出せました！

今回は、正六角形を使いましたが、これを正八角形や正12角形などにしていくと、さらに良い近似が可能です。

2003年の東京大学の入試で「円周率が3.05より大きいことを証明せよ」という問題が出題されましたが、これは正八角形を用いて同じように解くことが可能です。
※この問題を解くためには、三角比などの知識が必要です。

先ほどのように、ほぼ円に見える正多角形を使うと、より良い近似ができそうですよね。

下記サイトを使って計算してみると、正30角形で考えた場合は「円周率は3.135より大きい」、正40角形で考えた場合は「円周率は3.138より大きい」という結果が導き出せます。3.14にかなり近づいてきましたね！

※計算に使用したサイト：カシオ計算機株式会社　keisanサービス　円に内接する正多角形（2022/2/28参照）

まるで刺繍！曲線の長さの求め方

このように、刺繍のアイデアで長さを求められるのは円周だけではありません。

さまざまな丸みのある曲線の長さについても同じように考えることができます。

曲線上に、いくつか点を打ち、その点を縫い目のように直線でつないでいくことを考えてみましょう。

点が5個や10個など、少数の場合は、カクカクとした折れ線にしか見えないと思いますが、点の個数をできるだけ増やし、分割する幅をどんどん小さくすることで、元の曲線とそっくりな形状になっていくことでしょう。

そして、その縫い目一つ一つの長さを足し合わせることで、円周の場合のように、曲線の長さを知ることができそうですよね。

しかし、近似値ではなく、曲線の長さをきちんと知るためには「分割の幅を限りなく0に近づけること」と「無数にある折れ線の長さをすべて足し合わせること」という、非日常的な操作をしなければなりません。

そのときに役立つのが、微分積分なのです。

微分積分は「限りなく0に近づける」や「無数にあるものを足し合わせる」というアイデアを見事に実現してくれる素晴らしい手法です。

興味がある方は、高校の数学Ⅲのテキストや解析学の入門書を読んでみてくださいね。

刺繍からスタートして、円周率の近似、さらには微分積分の話にまでつながるなんて、ちょっと意外に感じられたかもしれません。

家庭科と数学、遠そうな存在なのに、しっかりと共通点があるんですね。

こうやって考えてみると、分野の垣根を越えて、知識を得ることは大切だと感じます。

もしも、この記事を読んでいるあなたが、数学に明るくなく、苦手意識があるのだとしたら……垣根を越えて学ぼうとする、素晴らしいモチベーションの持ち主です！

私自身も、そんなあなたの姿勢を見習って、数学に限らず、さまざまなことにリスペクトを持って学んでいこうと思います。

補足

実際には、曲線の長さは、非常に短い線分（本記事における縫い目）を用いた近似のアイデアによって定義されています。そのため、「曲線の長さを求めるために、細かな線分を用いる」というよりも、「そもそも、細かな線分によって、曲線の長さが定義されている」と言った方が正しいかもしれません。本記事では、このような厳密性よりも、幾何学的イメージによるわかりやすさを重視した説明をしています。

【正多角形の描画に使用したサイト】
Desmos　https://www.desmos.com/calculator?lang=ja